Modeling and Simulation Approaches

to Challenges in Nuclear Energy


Kathryn Huff

Rensselaer Polytechnic Institute

September 21, 2015

Physics, University of Chicago Nuclear Engineering and Engineering Physics, University of Wisconsin - Madison Nuclear Engineering, University of California, Berkeley
cyclus pyrk pyne pyrk Software Carpentry Scipy THW book

Insights at Disparate Scales

synergistic insights
image generated by Tommy Cisneros and the UCBerkeley FHR group
image generated by the UCBerkeley FHR group

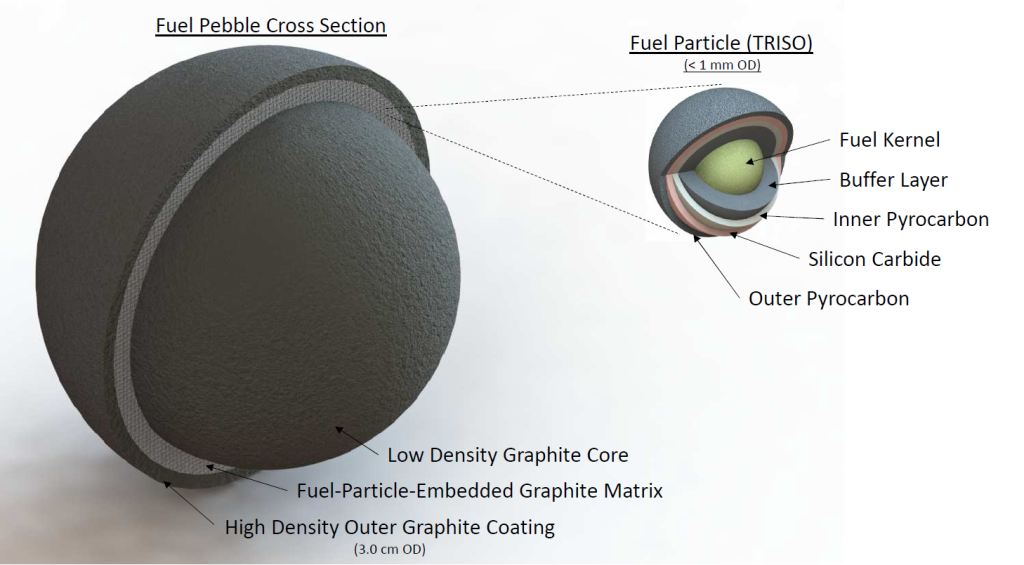
PB-FHR Fuel Geometry

FHR Pebbles diagram, UCB FHR project. This image from http://fhr.nuc.berkeley.edu/pb-fhr-technology/fuel-development/

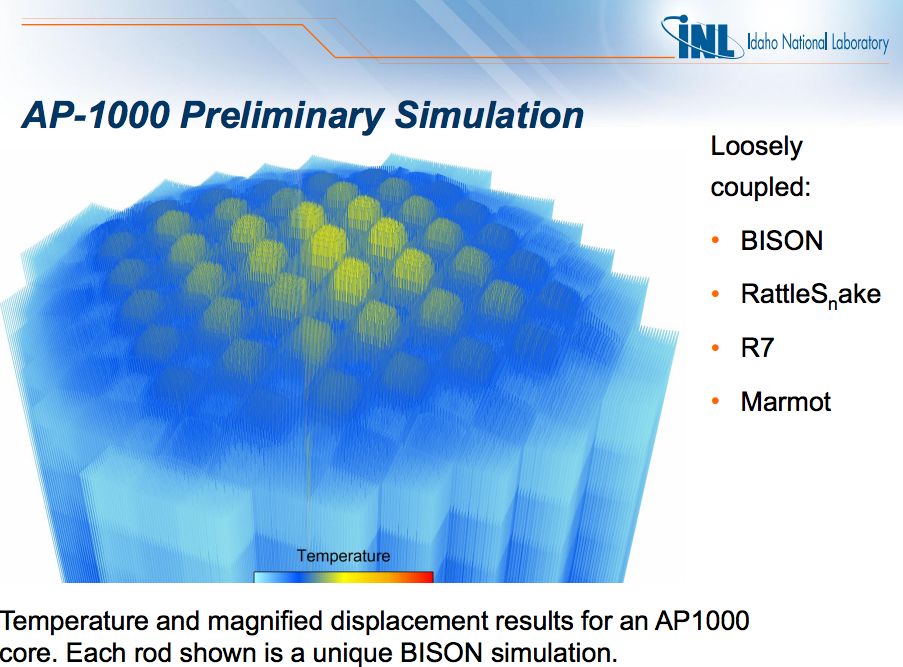
Coupled Multi-Physics Analysis


Severe accident neutronics and thermal hydraulics can be simulated beautifully for simple geometries and well studied materials. (below, INL BISON work.)

from INL, Rich Williamson

FHR, Accident Transient Analysis

  • Collect experimental data
  • Conduct algebraic, static, and benchmark results
  • Develop 0D coupled neutronics/TH model (PyRK)
  • Develop 3D neutronics/TH model
  • Compare 0D and 3D models
  • Connect additional coupled physics
pyrk
PyRK: Python for Reactor Kinetics

Review of Nuclear Reactor Kinetics

Fission.

\[\sigma(E,\vec{r},\hat{\Omega},T,x,i)\]

Chain reaction

\[k=1\]

Reactivity

\[ \begin{align} k &= \mbox{"neutron multiplication factor"}\\ &= \frac{\mbox{neutrons causing fission}}{\mbox{neutrons produced by fission}}\\ \rho &= \frac{k-1}{k}\\ \rho &= \mbox{reactivity}\\ \end{align} \]

Reactivity

\[ \rho(t) = \rho_0 + \rho_f(t) + \rho_{ext} \]
where
\[ \begin{align} \rho(t) &= \mbox{total reactivity}\\ \rho_f(t) &= \mbox{reactivity from feedback}\\ \rho_f(t) &= \sum_i \alpha_i\delta T_i\\ T_i &= \mbox{temperature of component i}\\ \alpha_i &= \mbox{temperature reactivity coefficient of i}\\ \rho_{ext}(t) &= \mbox{external reactivity insertion}. \end{align} \]
Feedback
Delayed Neutrons

\[\beta_i, \lambda_{d,i}\]

PyRK

  • 6-precursor-group,
  • 11-decay-group Point Reactor Kinetics model
  • Lumped Parameter thermal hydraulics model
  • Object-oriented, geometry and material agnostic framework

Point Reactor Kinetics

\[ \begin{align} p &= \mbox{ reactor power }\\ \rho(t,&T_{fuel},T_{cool},T_{mod}, T_{refl}) = \mbox{ reactivity}\\ \beta &= \mbox{ fraction of neutrons that are delayed}\\ \beta_j &= \mbox{ fraction of delayed neutrons from precursor group j}\\ \zeta_j &= \mbox{ concentration of precursors of group j}\\ \lambda_{d,j} &= \mbox{ decay constant of precursor group j}\\ \Lambda &= \mbox{ mean generation time }\\ \omega_k &= \mbox{ decay heat from FP group k}\\ \kappa_k &= \mbox{ heat per fission for decay FP group k}\\ \lambda_{FP,k} &= \mbox{ decay constant for decay FP group k}\\ T_i &= \mbox{ temperature of component i} \end{align} \]
\[ \frac{d}{dt}\left[ \begin{array}{c} p\\ \zeta_1\\ .\\ \zeta_j\\ .\\ \zeta_J\\ \omega_1\\ .\\ \omega_k\\ .\\ \omega_K\\ T_{i}\\ .\\ T_{I}\\ \end{array} \right] = \left[ \begin{array}{ c } \frac{\rho(t,T_{i},\cdots)-\beta}{\Lambda}p + \displaystyle\sum^{j=J}_{j=1}\lambda_{d,j}\zeta_j\\ \frac{\beta_1}{\Lambda} p - \lambda_{d,1}\zeta_1\\ .\\ \frac{\beta_j}{\Lambda}p-\lambda_{d,j}\zeta_j\\ .\\ \frac{\beta_J}{\Lambda}p-\lambda_{d,J}\zeta_J\\ \kappa_1p - \lambda_{FP,1}\omega_1\\ .\\ \kappa_kp - \lambda_{FP,k}\omega_k\\ .\\ \kappa_{k p} - \lambda_{FP,k}\omega_{k}\\ f_{i}(p, C_{p,i}, T_{i}, \cdots)\\ .\\ f_{I}(p, C_{p,I}, T_{I}, \cdots)\\ \end{array} \right] \]

Lumped Parameter Heat Transfer

The heat flow out of body $i$ is the sum of surface heat flow by conduction, convection, radiation, and other mechanisms to each adjacent body, $j$: \[ \begin{align} Q &= Q_i + \sum_j Q_{ij}\\ &=Q_i + \sum_j\frac{T_{i} - T_{j}}{R_{th,ij}}\\ \dot{Q} &= \mbox{total heat flow out of body i }[J\cdot s^{-1}]\\ Q_i &= \mbox{other heat transfer, a constant }[J\cdot s^{-1}]\\ T_i &= \mbox{temperature of body i }[K]\\ T_j &= \mbox{temperature of body j }[K]\\ j &= \mbox{adjacent bodies }[-]\\ R_{th} &= \mbox{thermal resistence of the component }[K \cdot s \cdot J^{-1}]. \end{align} \]

Quality Control

  • Unit Checking: Pint (github.com/pint)
  • Version Control: Git & GitHub (github.com/pyrk/pyrk)
  • Automated Documentation: Sphinx (pyrk.github.io)
  • Test Suite: nose
  • Continuous Integration: Travis (travis-ci.org/pyrk/pyrk)
  • Plotting: Matplotlib
  • ODE solvers: SciPy

Unit Checking

Pint
In PyRK, the Pint package (pint.readthedocs.org/en/0.6/) is used keeping track of units, converting between them, and throwing errors when unit conversions are not sane.

Version Control

Docs
Keeping track of versions of the code makes it possible to experiment without fear and placing the code online encourages use and collaboration.

Automated Documentation

Docs
Automated documentation creates a browsable website explaining the most recent version of the code.

Test Suite

Docs
The classes and functions that make up the code are tested individually for robustness using nose.

Continuous Integration

Docs
The tests are run every time a change is made to the repository online. The results are public. If a main branch has a failed test, I get an email.

Neutronics : Reactivity Insertion Model

reactivity
The reactivity insertion that drives the simulator can be selected and customized from three models.

PB-FHR Reactivity Insertion


Pebble-Bed, Fluoride Salt Cooled, High-Temperature Reactor
  • Molten FLiBe Coolant
  • Annular Core
  • Annular Pebble Fuel
  • Steady Inlet Temperature
  • Ramp Reactivity Insertion, 600pcm over 10s

Ramp Reactivity Insertion

reactivity insertion

Ramp Reactivity Insertion


# External Reactivity
from reactivity_insertion import RampReactivityInsertion
rho_ext = RampReactivityInsertion(timer=ti,
                                  t_start=t_feedback + 10.0*units.seconds,
                                  t_end=t_feedback + 20.0*units.seconds,
                                  rho_init=0.0*units.delta_k,
                                  rho_rise=600.0*units.pcm,
                                  rho_final=600.0*units.pcm)

Impulse Reactivity Insertion

reactivity pwer

Components



fuel = th.THComponent(name="fuel",
                      mat=Fuel,
                      vol=vol_fuel,
                      T0=t_fuel,
                      alpha_temp=alpha_fuel,
                      timer=ti,
                      heatgen=True,
                      power_tot=power_tot/n_pebbles,
                      sph=True,
                      ri=r_mod,
                      ro=r_fuel
                      )

mod = th.THComponent(name="mod",
                     mat=Moderator,
                     vol=vol_mod,
                     T0=t_mod,
                     alpha_temp=alpha_mod,
                     timer=ti,
                     sph=True,
                     ri=0.0,
                     ro=r_mod)

cool = th.THComponent(name="cool",
                      mat=cool,
                      vol=vol_cool,
                      T0=t_cool,
                      alpha_temp=alpha_cool,
                      timer=ti)

shell = th.THComponent(name="shell",
                       mat=Shell,
                       vol=vol_shell,
                       T0=t_shell,
                       alpha_temp=alpha_shell,
                       timer=ti,
                       sph=True,
                       ri=r_fuel,
                       ro=r_shell)

Heat Transfer


# The coolant convects to the pebbles
cool.add_convection('pebble', h=h_cool, area=a_pb)
cool.add_advection('cool', m_flow/n_pebbles, t_inlet, cp=cool.cp)

Pebble Temperature

reactivity Temperatures

Average fuel pebble peak temperature \[<1100^\circ C\]

image generated by Anthony Scopatz, Paul P.H. Wilson, and Katy Huff

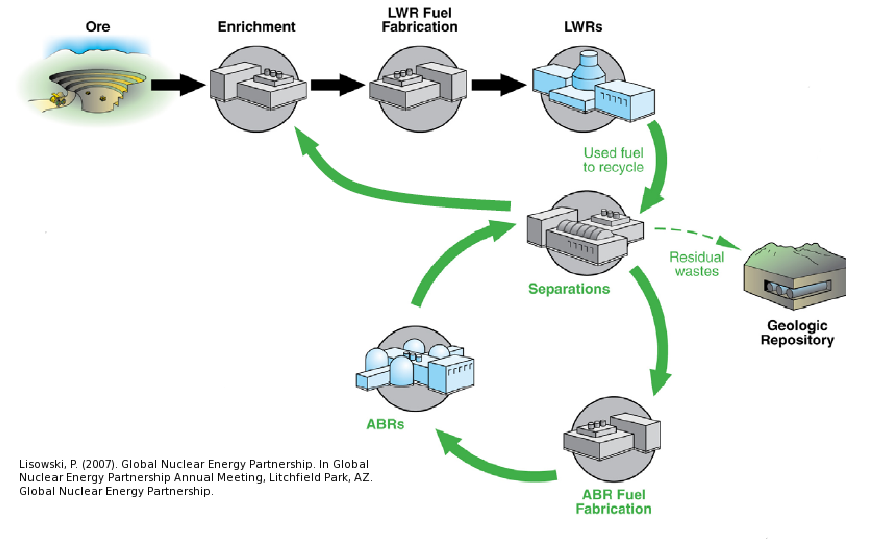
A Nuclear Fuel Cycle Simulation Framework

The Nuclear Fuel Cycle

Hundreds of discrete facilities mine, mill, convert, fabricate, transmute, recycle, and store nuclear material.

from Paul Lisowski

Fuel Cycle Metrics

  • Mass Flow
    • inventories, decay heat, radiotoxicity,
    • proliferation resistance and physical protection (PRPP) indices.
  • Cost
    • levelized cost of electricity,
    • facility life cycle costs.
  • Economics
    • power production, facility deployments,
    • dynamic pricing and feedback.
  • Disruptions
    • reliability, safety,
    • system robustness.

Current Simulators

  • CAFCA (MIT)
  • COSI (CEA)
  • DANESS (ANL)
  • DESAE (Rosatom)
  • Evolcode (CIEMAT)
  • FAMILY (IAEA)
  • GENIUSv1 (INL)
  • GENIUS v2 (UW)
  • NFCSim (LANL)
  • NFCSS (IAEA)
  • NUWASTE (NWTRB)
  • ORION (NNL)
  • MARKAL (BNL)
  • VISION (INL)

State of the Art

Performance

  • Speed interactive time scales
  • Fidelity: detail commensurate with existing challenges
  • Detail: discrete material and agent tracking
  • Regional Modeling: enabling international socio-economics

Beyond the State of the Art

Access

  • Openness: for collaboration, validation, and code sustainability.
  • Usability: for a wide range of user sophistication

Extensibility

  • Modularity: core infrastructure independent of proprietary or sensitive data and models
  • Flexibility with a focus on robustness for myriad potential developer extensions.

Extensibility

framework

Openness

private, export controlled, etc.

...Well Beyond

Algorithmic Sophistication

  • Efficient: memory-efficient isotope tracking
  • Customizable: constrained fuel supply
  • Dynamic: isotopic-quality-based resource routing
  • Physics-based: fuel fungibility

Agent Based Systems Analysis

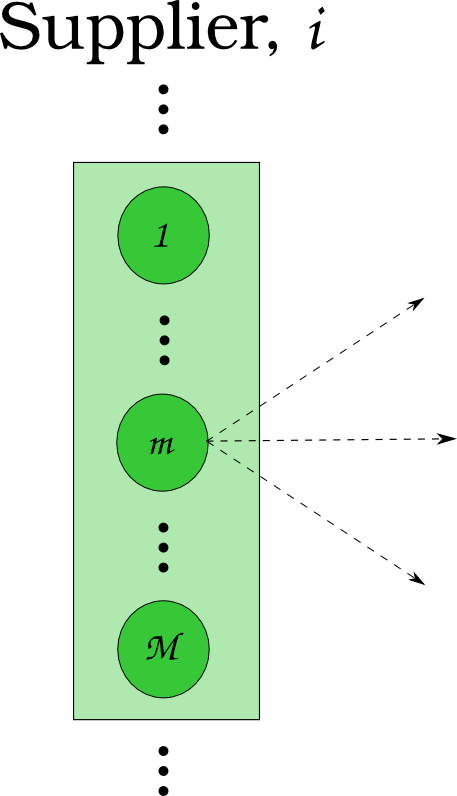
An agent-based simulation is made up of actors and communications between those actors.

from Paul Lisowski

Agent Based Systems Analysis

A facility might create material.

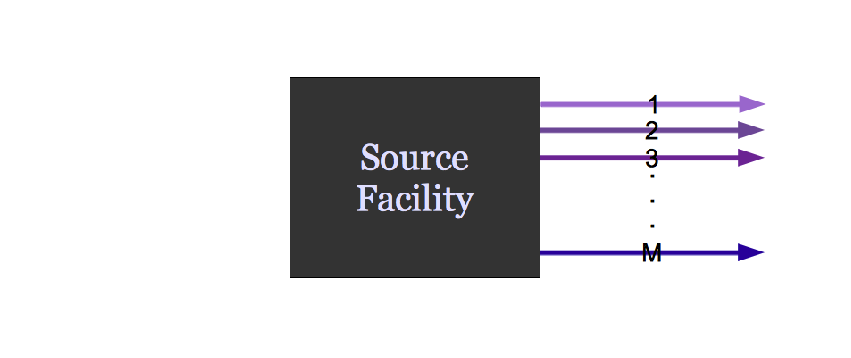
source

Agent Based Systems Analysis

It might request material.

sink

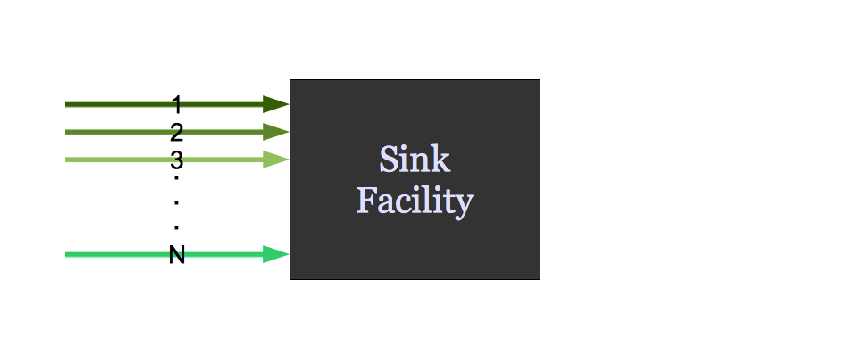
Agent Based Systems Analysis

It might do both.

fac

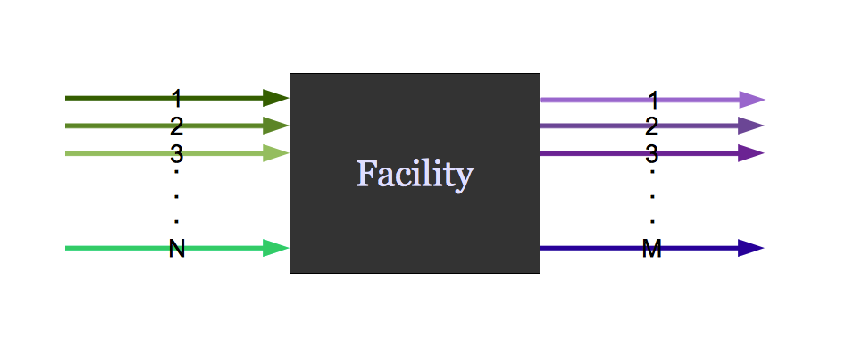
Agent Based Systems Analysis

Even simple fuel cycles have many independent agents.

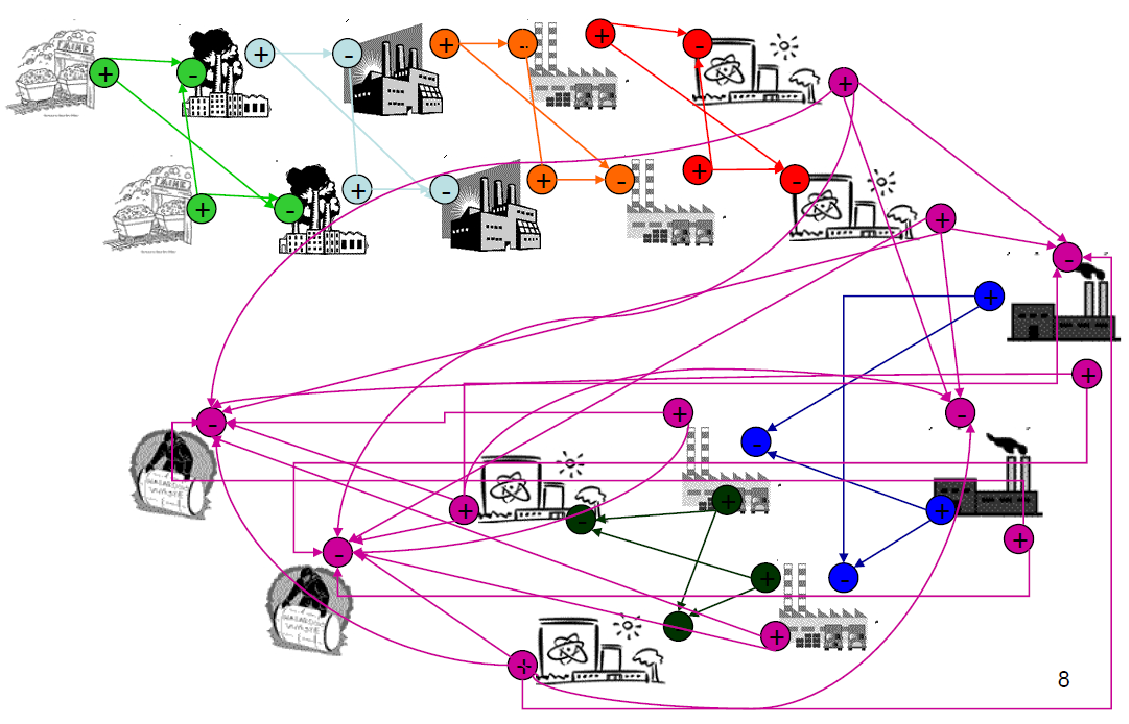
material flow

Agent Based Systems Analysis

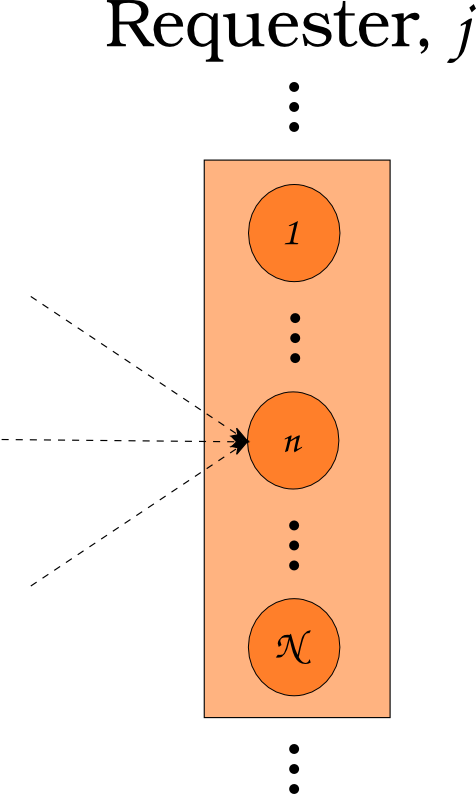abm \[N_i \subset N\]

Agent Based Systems Analysis

abm \[N_j \subset N\]

Agent Based Systems Analysis

abm \[N_i \cup N_j = N\]

Feasibility vs. Optimization

polynomial hardness

If a decision problem is in NP-C, then the corresponding optimization problem is NP-hard.

Transportation Formulation

multicommoditiy transportation problem formulation multicommoditiy transportation problem formulation

Transportation Formulation


\[ \begin{align} \min_{x} z &= \sum_{i\in I}\sum_{j\in J} c_{i,j}x_{i,j} & \\ s.t & \sum_{i\in I_s}\sum_{j\in J} a_{i,j}^k x_{i,j} \le b_s^k & \forall k\in K_s, \forall s\in S\\ & \sum_{J\in J_r}\sum_{i\in I} a_{i,j}^k x_{i,j} \le b_r^k & \forall k\in K_r, \forall r\in R\\ & x_{i,j} \in [0,x_j & \forall i\in I, \forall j\in J \end{align} \]

Growing Ecosystem


a growing number of scientists are adding modules to cyclus.
Canonical Comparisons

Insights at Disparate Scales

synergistic insights

Detailed Metrics

possible metrics

Material Attractiveness

possible metrics

Insights at Disparate Scales

synergistic insights

Links

Acknowledgements

  • Matthew Gidden
  • Anthony Scopatz
  • Massimiliano Fratoni
  • Ehud Greenspan
  • Per Peterson
  • Xin Wang
  • Paul Wilson
  • Jasmina Vujic

BIDS Logo FHR Logo

THE END

Katy Huff

katyhuff.github.io/2015-09-21-rpi
Creative Commons License
Modeling and Simulation Approaches to Challenges in Nuclear Energy by Kathryn Huff is licensed under a Creative Commons Attribution 4.0 International License.
Based on a work at http://katyhuff.github.io/2015-09-21-rpi.