Data in Nuclear Engineering
Kathryn (Katy) Huff
















\[\phi(E,\vec{r},\hat{\Omega},T)\]
\[\phi(E, x, y, z, \theta, \omega, T)\]

\[\sigma(x, i, E, T)\]

\[\gamma(f, i)\]
\[i\]
\[E\]

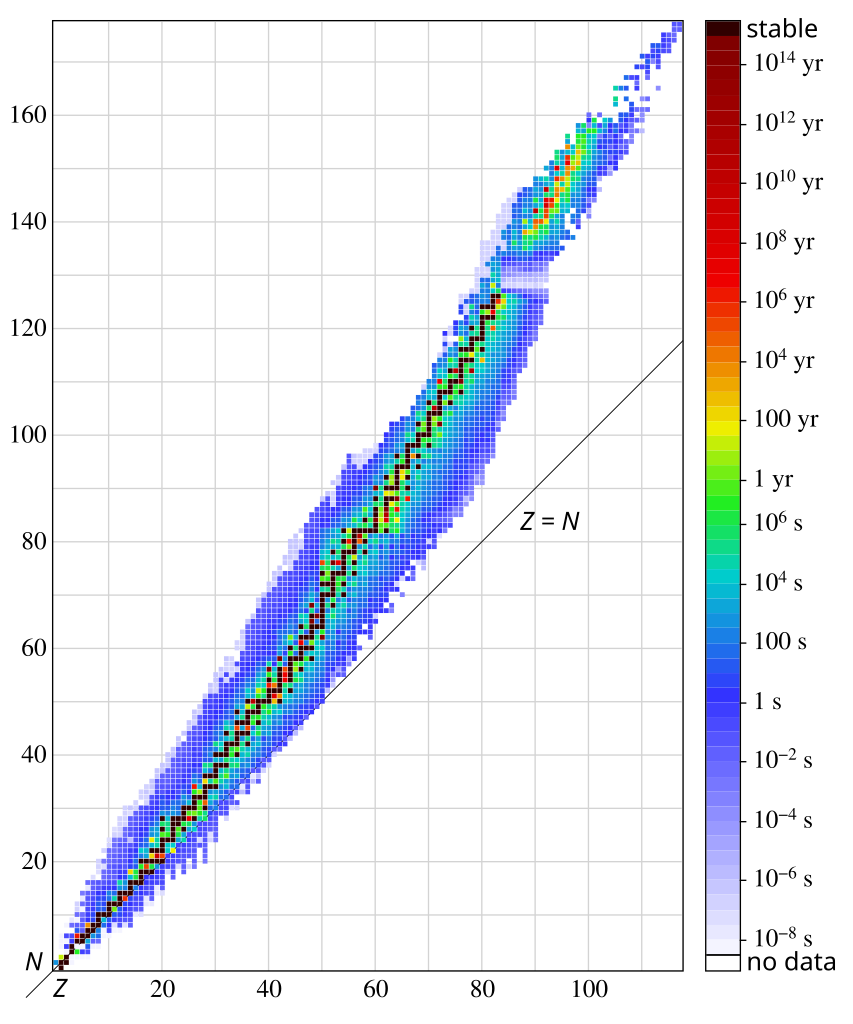
nuclear structure
Evaluated Nuclear Data Sets
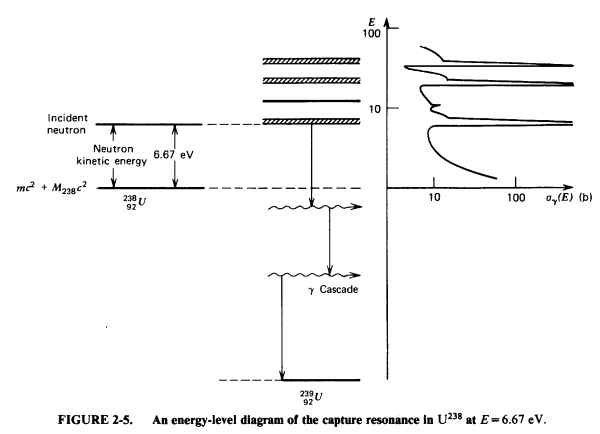
\[\sigma(x, i, E, T)=\] nuclear structure + experiments
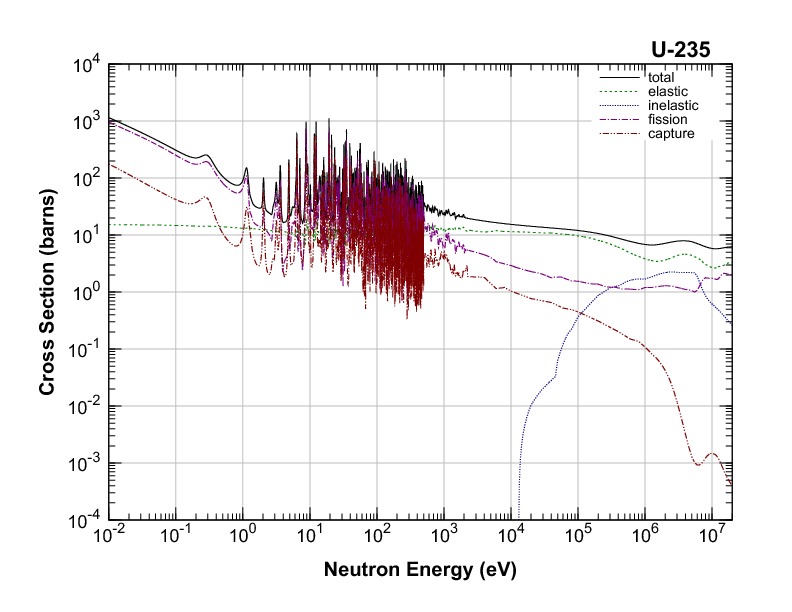
Experiments
Experiments

Nuclear Data is for Simulations




Simulation Methods
- Monte Carlo Methods
- Deterministic Methods
- Hybrid Methods
- Other keywords...
- lattice codes
- ray tracing algorithms
- acceleration schemes
- adjoint methods
- ...
Application Specific Data Processing
- Energy discretization
- multigroup
- pointwise
- piecewise linear continuous
- Angular quadratures
- Resonance integration
- ...
Molten Salt Reactor Designs

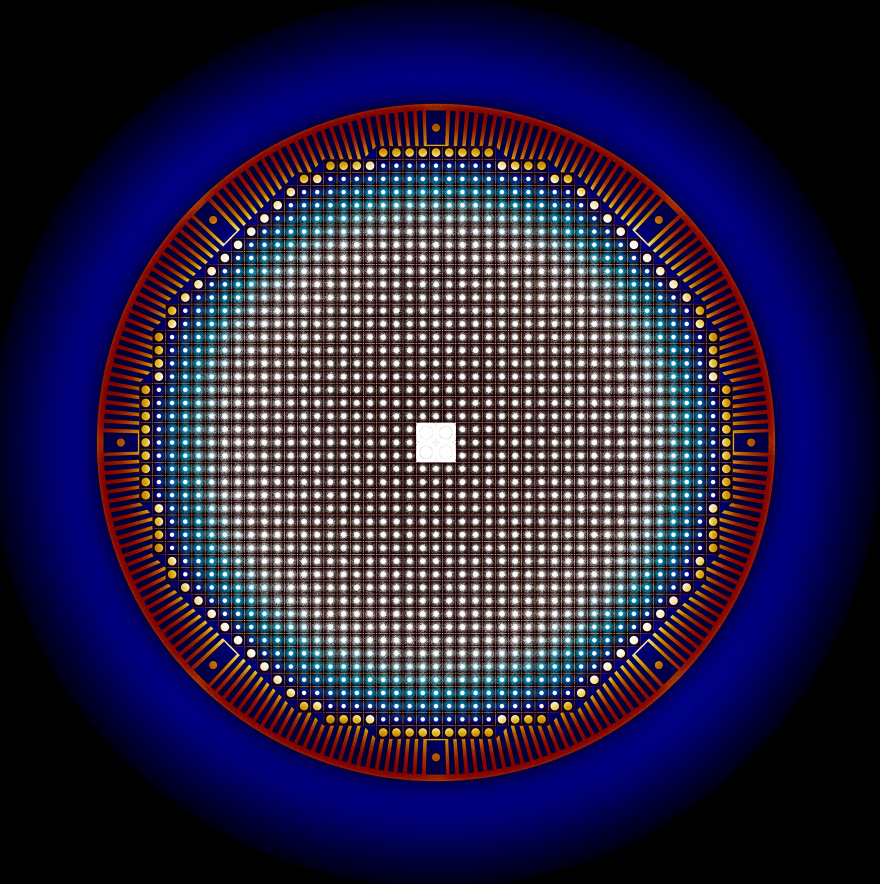
MSBR Full Core Simulation
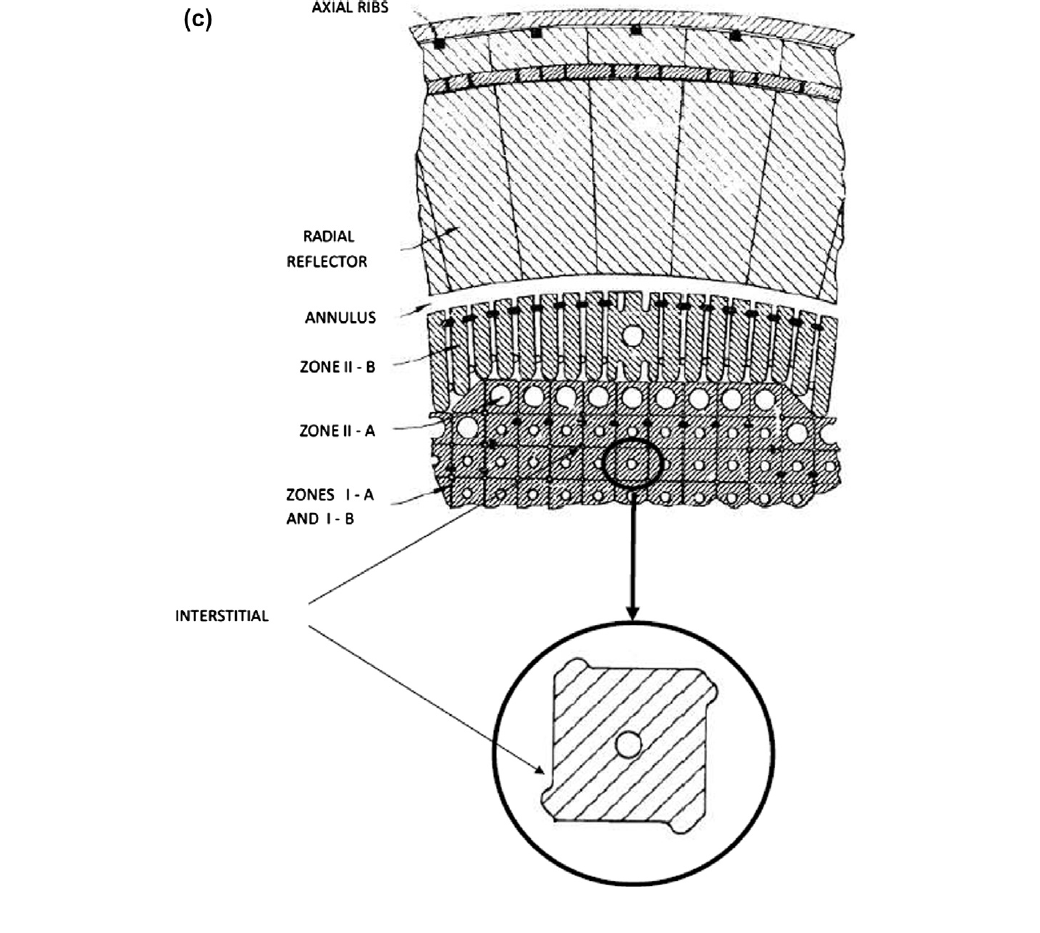
(Robertson, 1979)
MSBR Full Core Simulation
Andrei Rykhlevskii

MSBR Full Core Simulation
Andrei Rykhlevskii

MSBR Full Core Simulation
Andrei Rykhlevskii
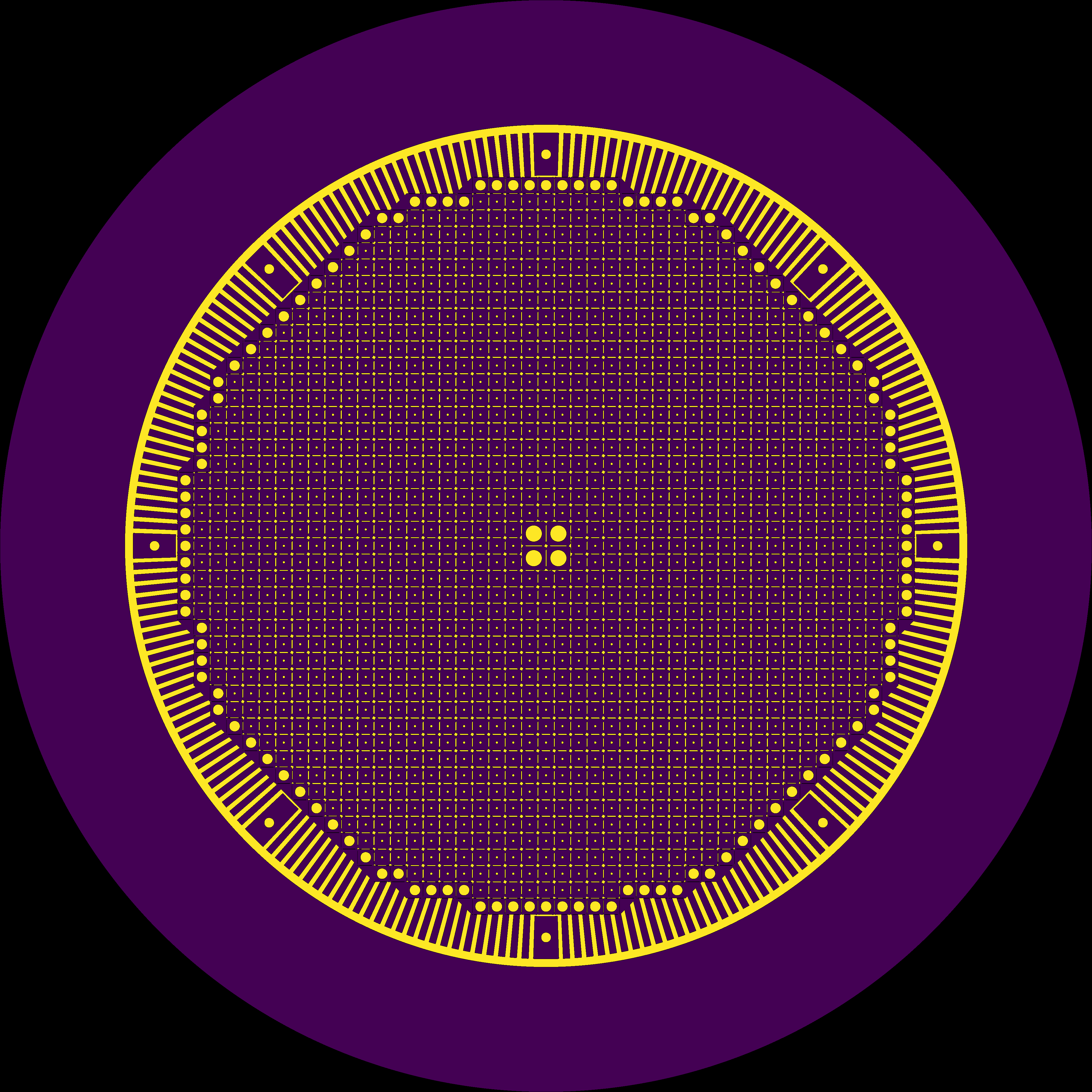
MSBR Full Core Simulation
Andrei Rykhlevskii

MSBR Full Core Simulation
Andrei Rykhlevskii
MSBR Full Core Simulation
Andrei Rykhlevskii
MSBR Full Core Simulation
Andrei Rykhlevskii
MSBR Full Core Simulation
Andrei Rykhlevskii
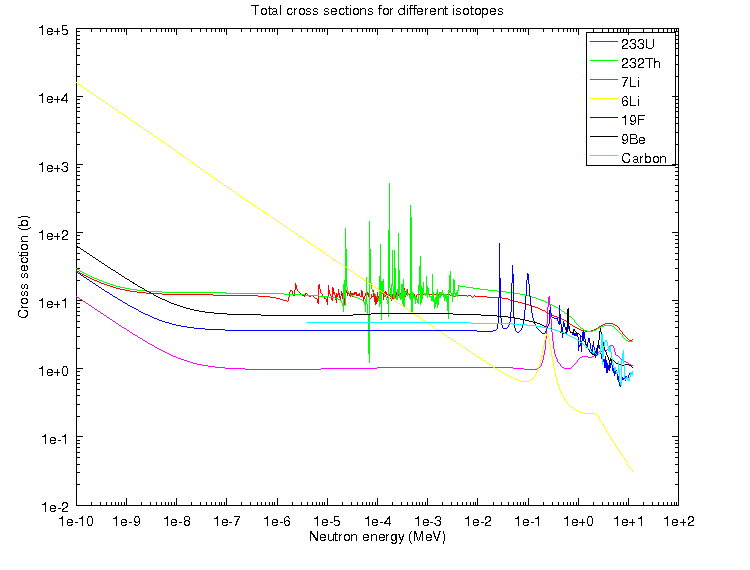
MSBR Full Core Simulation
Andrei Rykhlevskii
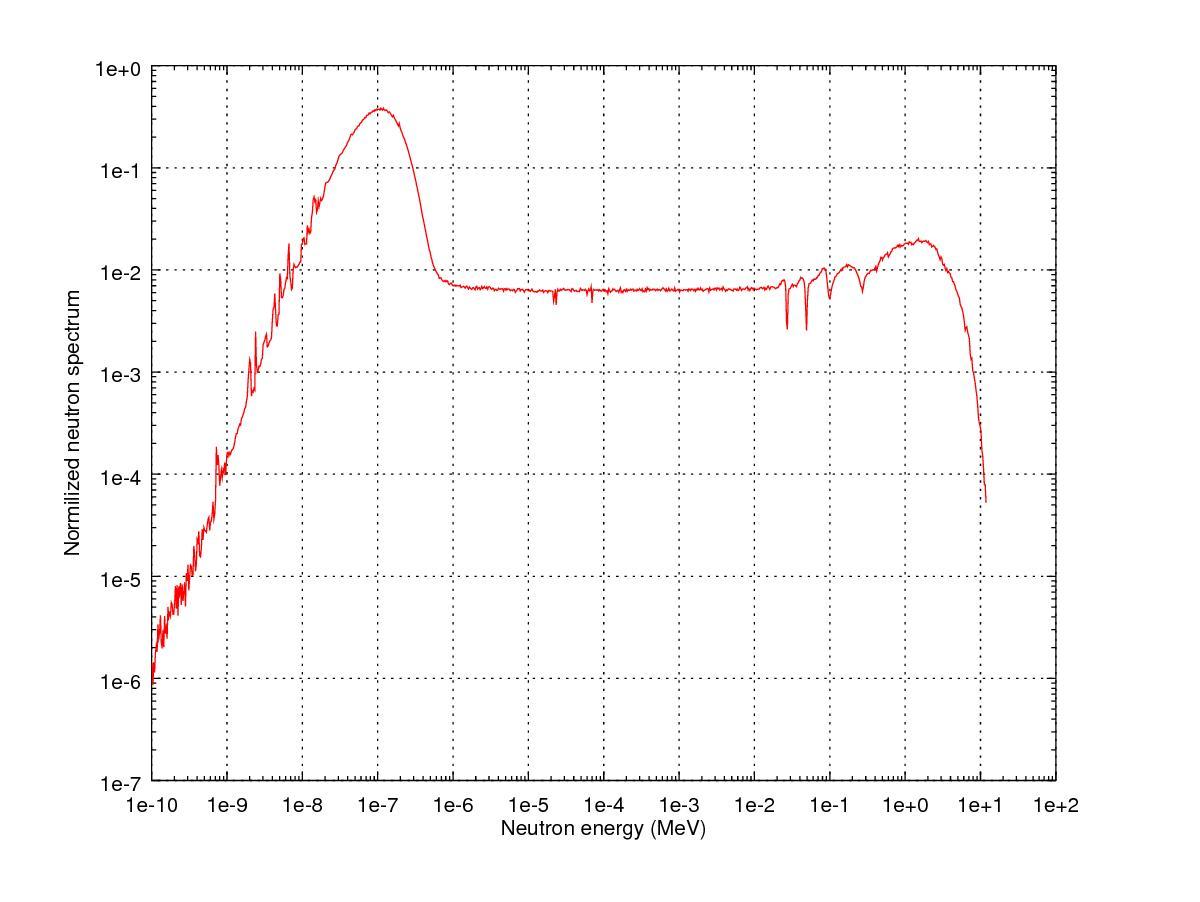
Reactor Kinetics

\[\sigma(E,\vec{r},\hat{\Omega},T,x,i)\]

\[k=1\]
Reactivity
\[ \begin{align} k &= \mbox{"neutron multiplication factor"}\\ &= \frac{\mbox{neutrons causing fission}}{\mbox{neutrons produced by fission}}\\ \rho &= \frac{k-1}{k}\\ \rho &= \mbox{reactivity}\\ \end{align} \]

\[\beta_i, \lambda_{d,i}\]
Point Reactor Kinetics
\[ \begin{align} p &= \mbox{ reactor power }\\ \rho(t,&T_{fuel},T_{cool},T_{mod}, T_{refl}) = \mbox{ reactivity}\\ \beta &= \mbox{ fraction of neutrons that are delayed}\\ \beta_j &= \mbox{ fraction of delayed neutrons from precursor group j}\\ \zeta_j &= \mbox{ concentration of precursors of group j}\\ \lambda_{d,j} &= \mbox{ decay constant of precursor group j}\\ \Lambda &= \mbox{ mean generation time }\\ \omega_k &= \mbox{ decay heat from FP group k}\\ \kappa_k &= \mbox{ heat per fission for decay FP group k}\\ \lambda_{FP,k} &= \mbox{ decay constant for decay FP group k}\\ T_i &= \mbox{ temperature of component i} \end{align} \]
Coupled Multi-Physics Analysis
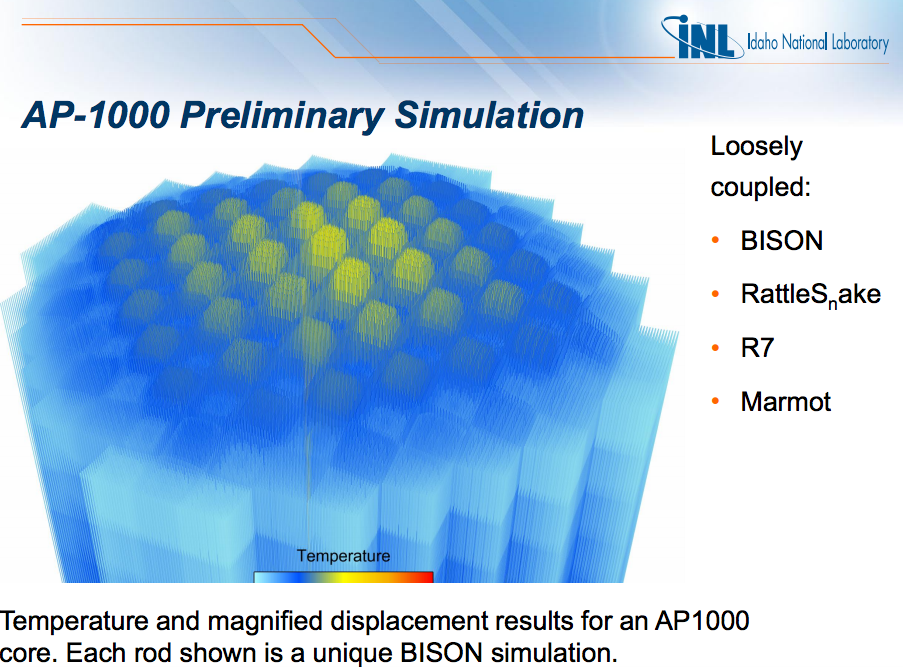
Using the MOOSE framework and its Jacobian-Free Newton Krylov solver, severe accident neutronics and thermal hydraulics can be simulated beautifully for simple geometries and well studied materials. (below, INL BISON work.)
Moltres: Dr. Alexander Lindsay

Moltres Current Capabilities
- Navier Stokes + Multi-Group Neutron Diffusion + Kinetics
- arbitrary number of neutron energy groups
- arbitrary number of delayed neutron precursor groups
- neutron power coupled to salt temperature and flow
- Precursor capability requires discontinuous galerkin upwind scheme.
- Few group constants can be generated with SCALE-NEWT or Serpent
MSR Neutronics and TH Coupling
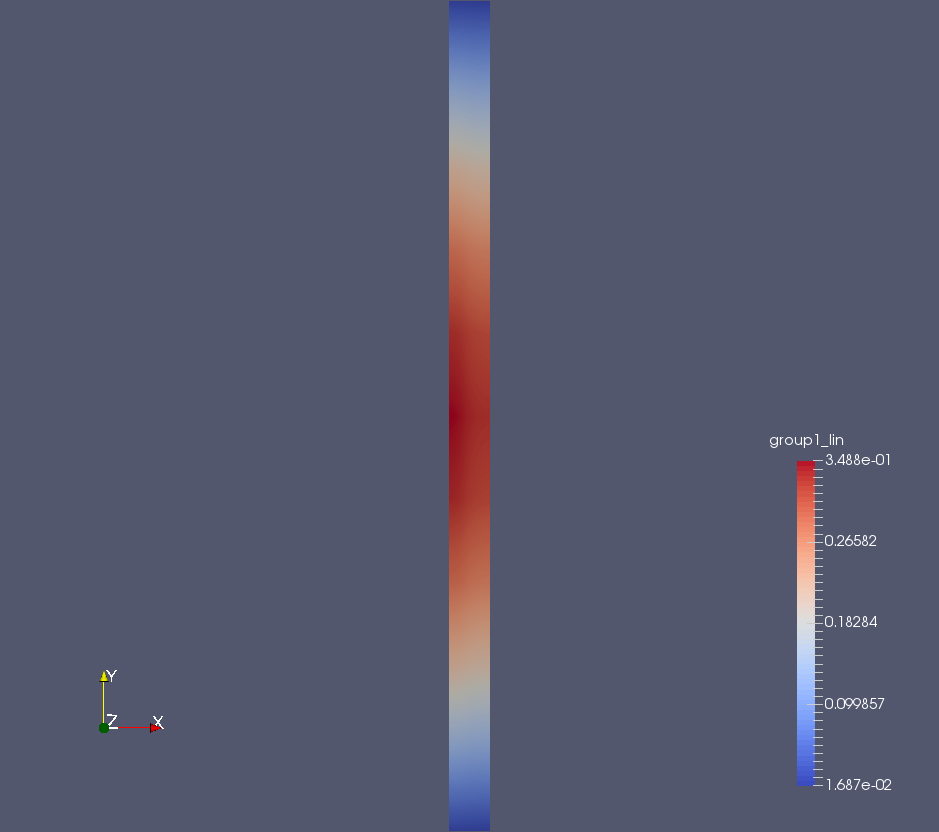
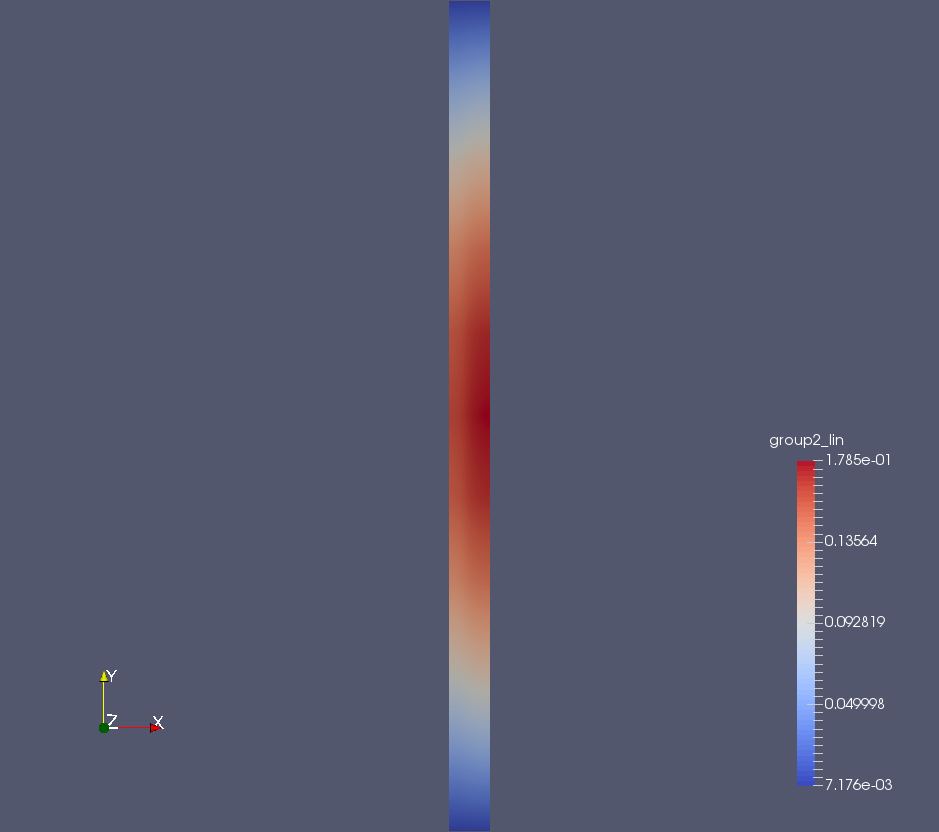
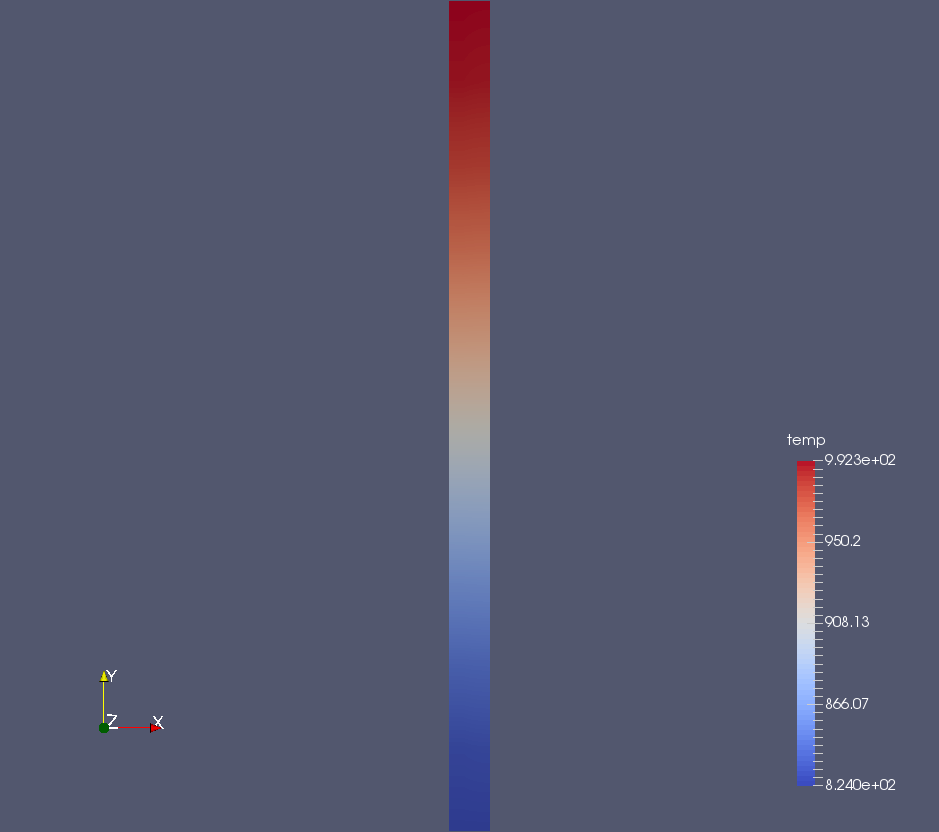
MSR Precursors
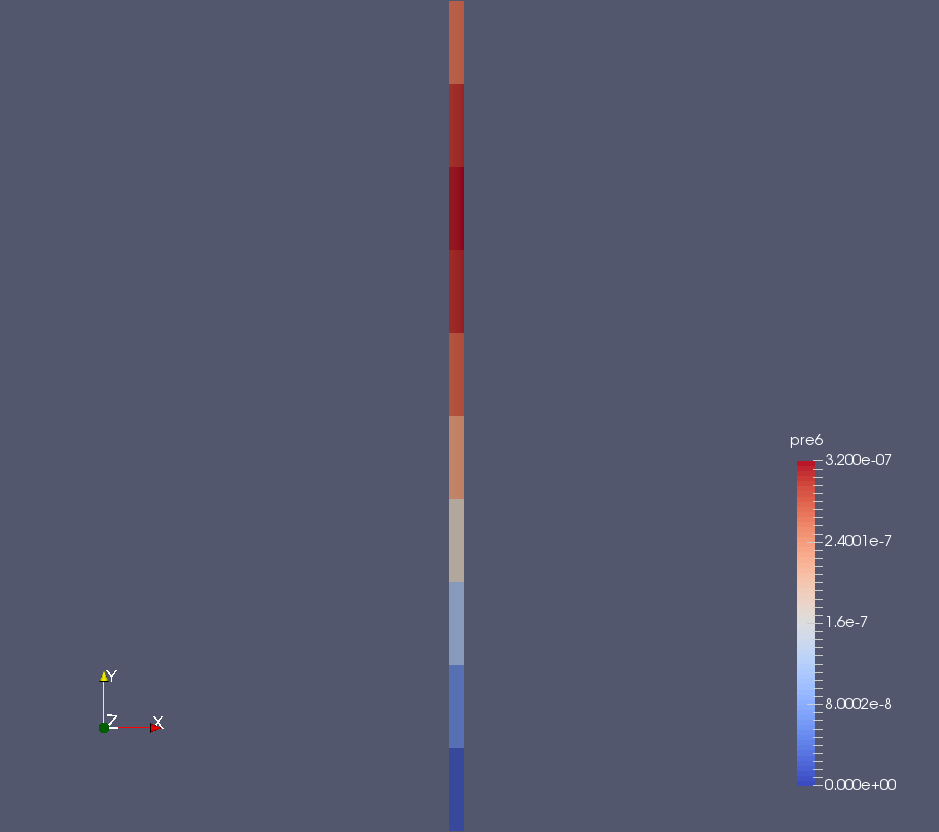
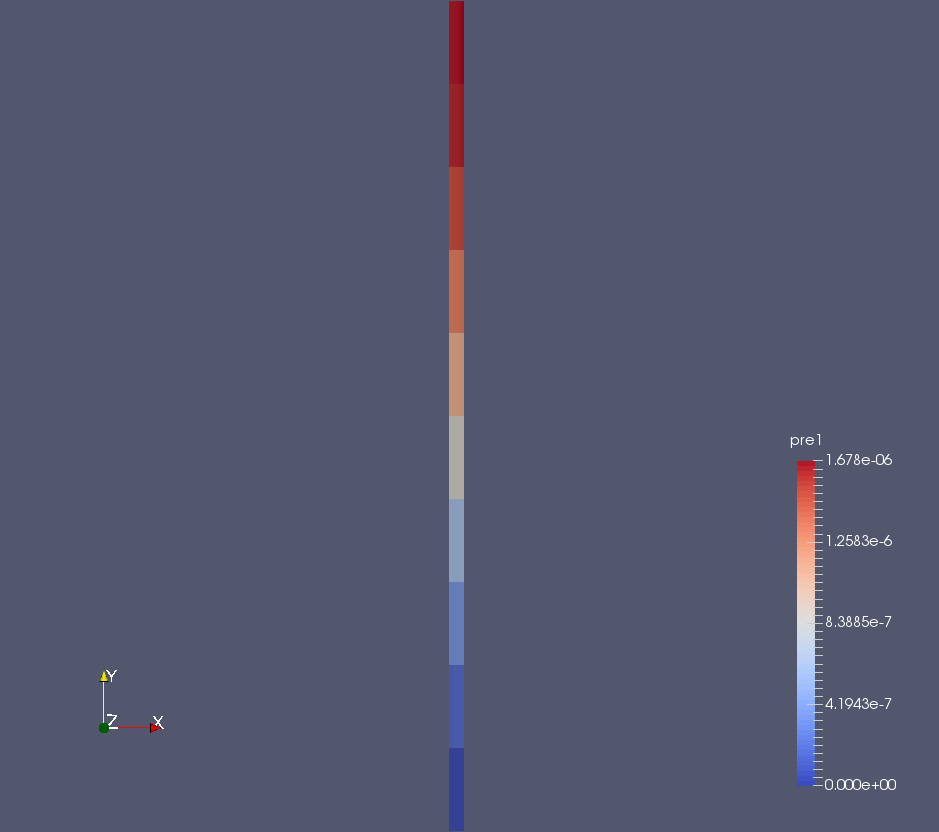
How Do We Know It's Right?

The Data Dilemma

Unique Issues
Export control is serious.
Links
THE END
Katy Huff
katyhuff.github.io/2017-05-31-pi4
Data in Nuclear Engineering by Kathryn Huff is licensed under a Creative Commons Attribution 4.0 International License.
Based on a work at http://katyhuff.github.io/2017-05-31-pi4.
A Few of My Favorite Things
- C++, Python, Fortran
- xml, markdown, rst, $\LaTeX$
- Doxygen, sphinx
- CMake, conda, macports
- GoogleTest, nose
- hdf5, sqlite
- cython, boost, Coin
- jekyll, reveal.js, beamer
- yt, matplotlib, paraview
