FHR Coupled, Transient Analysis

Collect experimental data
Conduct algebraic, static, and benchmark simulations
Develop few group parameters, steady state results
Develop 0D coupled neutronics/TH model (PyRK)
Develop 3D neutronics/TH model
Compare 0D and 3D simulations
Couple additional physics (e.g. fuel performance)

MOOSE-Based Application Development

MOOSE Framework

Finite Element Framework
Jacobian-Free Newton Krylov
Adaptively meshed geometry handling
Scalability

PRONGHORN Capabilities

Diffusion Neutronics
Conjugate Heat Transfer
Pebble Bed Darcy Flow (gaseous)

PRONGHORN PBMR-400 Benchmark

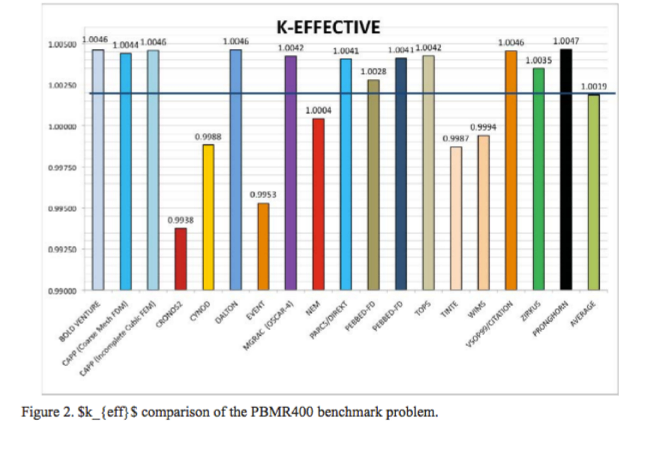
Single-Phase, Incompressible, Thermally-Expandable Flow

Continuity

\[ \begin{align} \frac{\partial \epsilon \rho_f}{\partial t} + \nabla(\epsilon \rho_f \vec{u}) &= 0\\ \end{align} \]

Momentum

\[ \begin{align} \frac{\partial \epsilon \rho_f}{\partial t} + \nabla(\epsilon \rho_f \vec{u}\times\vec{u}) + \nabla \epsilon P - \epsilon \rho_f \vec{g} + W\rho_f\vec{u} =0\\ \end{align} \]

Energy

\[ \begin{align} \frac{\partial\epsilon\rho_fH}{\partial t} + \nabla(\epsilon\rho_f\vec{u}H) &= q''' \end{align} \]

This form of the energy equation can be simplified with the introduction of the specific heat capacity, $C_p = \frac{\partial H}{\partial T}$. This nonconservative assumption results in a form of the energy equation appropriate for incompressible or nearly incompressible flows. \[ \begin{align} \rho C_p\frac{\partial T}{\partial t} + \rho C_p \vec{u} \nabla T &= q''' \end{align} \]

These equations are closed by the equation of state. This can be either of the form $P=P(\rho, \rho\vec{u}, \rho\vec{E})$ or $\rho=\rho(P, T)$. To ensure incompressible, thermally expandable flow, as in Hu, we use a relation between density and temperature of the form: \[ \begin{align} \frac{\partial \rho}{\partial t} &= \xi \frac{\partial T}{\partial t}\\ \nabla \rho &= \xi \nabla T \end{align} \]

Single-Phase, Incompressible, Thermally-Expandable Flow

Stabilization (SUPG/PSPG)

\[ \left\langle f_{continuity},\psi\right\rangle+\left\langle f_{mom,non},\tau_{pspg}\times\nabla\psi\right\rangle\\ \left\langle f_{mom},\psi\right\rangle+\left\langle f_{mom,non},\tau_{supg}\times\nabla\psi\right\rangle\\ \left\langle f_{energy},\psi\right\rangle+\left\langle f_{energy,non},\tau_{supg}\times\nabla\psi\right\rangle \]