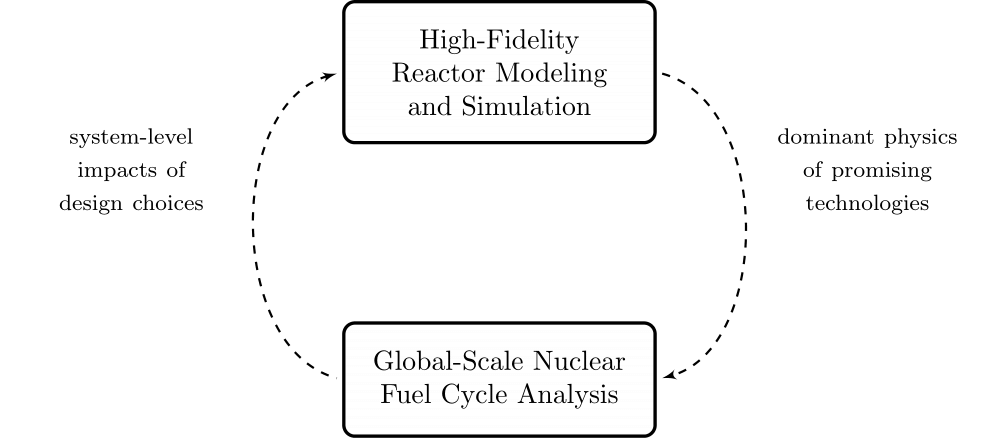
Modeling and Simulation at Disparate Scales

Molten Salt Reactor Multiphysics and International Fuel Cycle Transitions


Kathryn (Katy) Huff

UM NERS Colloquium, 2018.02.16

Physics, University of Chicago Nuclear Engineering and Engineering Physics, University of Wisconsin - Madison Nuclear Engineering, University of California, Berkeley Illinois
ARFC Logo
cyclus pyrk pyne MOOSE

Insights at Disparate Scales

synergistic insights

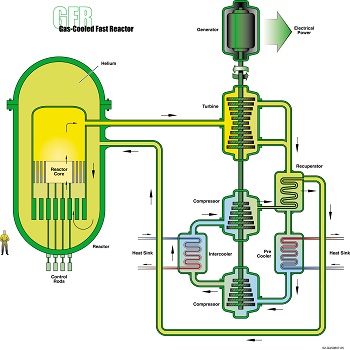
Advanced Reactors

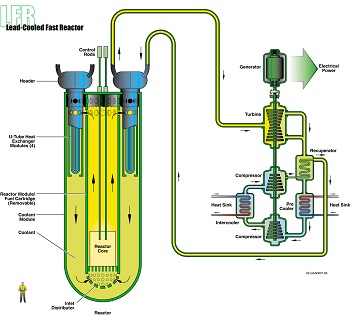
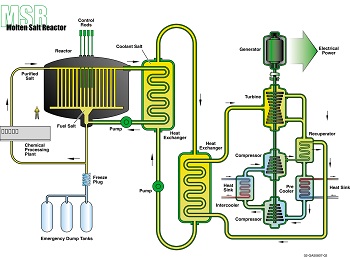
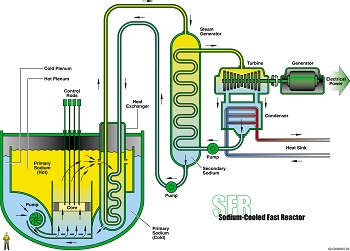
adv reactors, gen 4 adv reactors, gen 4
adv reactors, gen 4 adv reactors, gen 4

MOOSE Framework

synergistic insights

Moltres (coupling in MOOSE)

Alexander Lindsay, Kathryn Huff

Intro to Moltres/MOOSE

  • Fluid-fuelled, molten salt reactors
  • Multi-group diffusion (arbitrary groups)
  • Advective movement of delayed neutron precursors
  • Navier-Stokes thermal hydraulics
  • 3D unstructured
  • 2D axisymmetric
  • 3D structured

Acquiring Moltres


git clone https://github.com/arfc/moltres
cd moltres
git submodule init
git submodule update

Acquiring Moltres

Moltres is built atop the Multi-physics Object-Oriented Simulation Environment (MOOSE) (Gaston et al.).

  • MOOSE interfaces with libMesh to discretize simulation volume into finite elements
  • Provides interface for coding residuals that correspond to weak form of governing PDEs; also interface for coding Jacobians → more accurate Jacobians → more efficient convergence
  • Residuals and Jacobians handed off to PetSc which handles solution of resulting non-linear system of algebraic equations

In Moltres, neutrons are described with time-dependent multi-group diffusion:

\[ \begin{align} \frac{1}{v_g}\frac{\partial \phi_g}{\partial t} &- \nabla \cdot D_g \nabla \phi_g + \Sigma_g^r \phi_g = \sum_{g \ne g'}^G \Sigma_{g'\rightarrow g}^s \phi_{g'} + \chi_g^p \sum_{g' = 1}^G (1 - \beta) \nu \Sigma_{g'}^f \phi_{g'} + \chi_g^d \sum_i^I \lambda_i C_i \end{align} \]
\[ \begin{align} v_g &= \mbox{speed of neutrons in group g} \\ \phi_g &= \mbox{flux of neutrons in group g} \\ t &= \mbox{time} \\ D_g &= \mbox{Diffusion coefficient for neutrons in group g} \\ \Sigma_g^r &= \mbox{macroscopic cross-section for removal of neutrons from group g} \\ \Sigma_{g'\rightarrow g}^s &= \mbox{macroscopic cross-section of scattering from g' to g} \\ \chi_g^p &= \mbox{prompt fission spectrum, neutrons in group g} \\ G &= \mbox{number of discrete groups, g} \\ \nu &= \mbox{number of neutrons produced per fission} \\ \Sigma_g^f &= \mbox{macroscopic cross section for fission due to neutrons in group g} \\ \chi_g^d &= \mbox{delayed fission spectrum, neutrons in group g} \\ I &= \mbox{number of delayed neutron precursor groups} \\ \beta &= \mbox{delayed neutron fraction}\\ \lambda_i &= \mbox{average decay constant of delayed neutron precursors in precursor group i} \\ C_i &= \mbox{concentration of delayed neutron precursors in precursor group i} . \end{align} \]

Delayed neutron precursors are described to include a term representing the effect of fuel advection.

\[ \begin{align} \frac{\partial C_i}{\partial t} &= \sum_{g'= 1}^G \beta_i \nu \Sigma_{g'}^f \phi_{g'} - \lambda_i C_i - \frac{\partial}{\partial z} u C_i \label{eq:precursors} \end{align} \]
The governing equation for the fuel temperature is modeled as: \[ \begin{align} \rho_fc_{p,f}\frac{\partial T_f}{\partial t} &+ \nabla\cdot\left(\rho_f c_{p,f} \vec{u}\cdot T_f -k_f\nabla T_f\right) = Q_f \end{align} \] \[ \begin{align} \rho_f &= \mbox{density of fuel salt}\\ c_{p,f} &= \mbox{specific heat capacity of fuel salt}\\ T_f &= \mbox{temperature of fuel salt}\\ \vec{u} &= \mbox{velocity of fuel salt}\\ k_f &= \mbox{thermal conductivity of fuel salt}\\ Q_f &= \mbox{source term} = \sum_{g=1}^G \epsilon_{f,g}\Sigma_{f,g}\phi_g \end{align} \]
In the moderator, the governing equation for temperature is given by: \[\begin{align} \rho_gc_{p,g}\frac{\partial T_g}{\partial t} &+ \nabla\cdot\left(-k_g\nabla T_g\right) = Q_g\\ \end{align} \] \[ \begin{align} \rho_g &= \mbox{density of graphite moderator}\\ c_{p,g} &= \mbox{specific heat capacity of graphite moderator}\\ T_g &= \mbox{temperature of graphite moderator}\\ k_g &= \mbox{thermal conductivity of graphite moderator}\\ Q_g &= \mbox{source term in graphite moderator}\\ \end{align} \]

Moltres MSRE Simulation

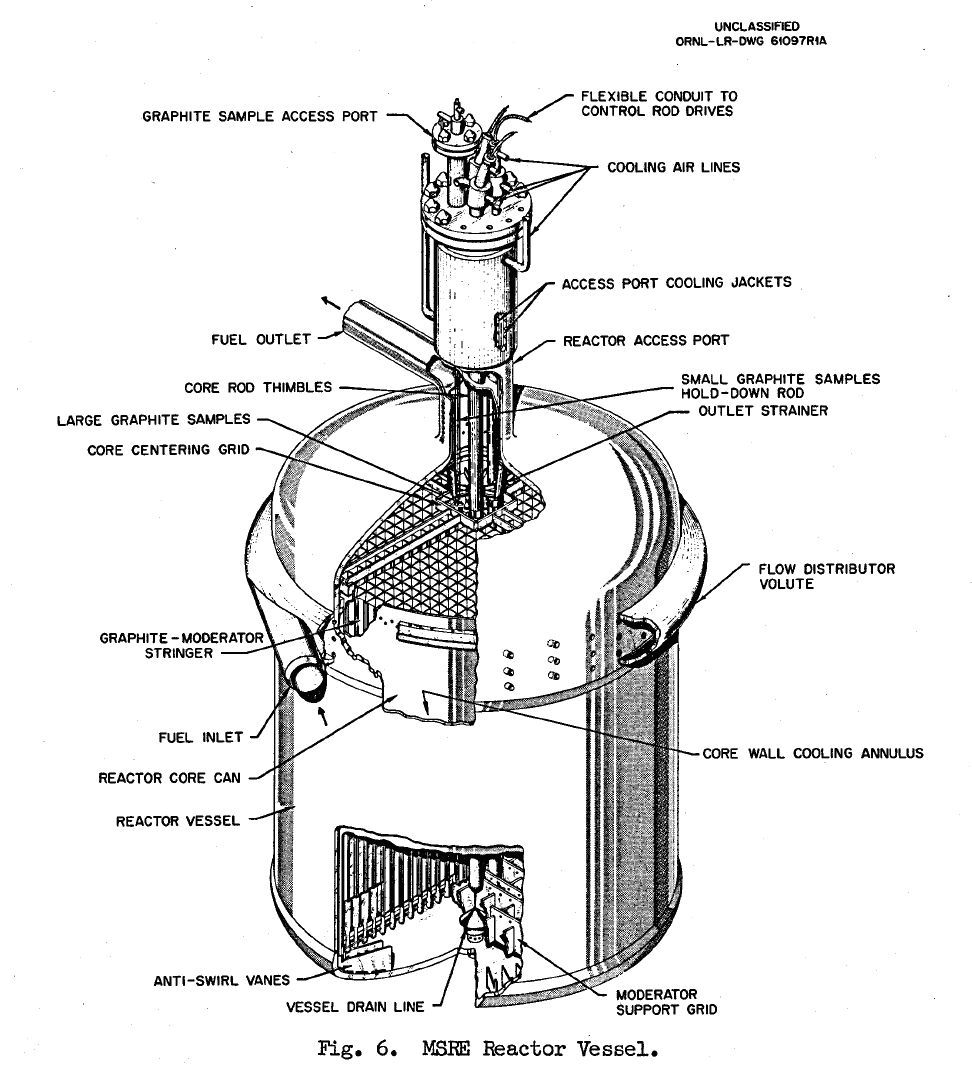
Moltres MSRE Simulation

Alexander Lindsay, Kathryn Huff

Moltres MSRE Simulation

Alexander Lindsay, Kathryn Huff

Moltres (coupling in MOOSE)

Alexander Lindsay, MSRE serpent simulation
Alexander Lindsay, 2016

Moltres Precursor Drift

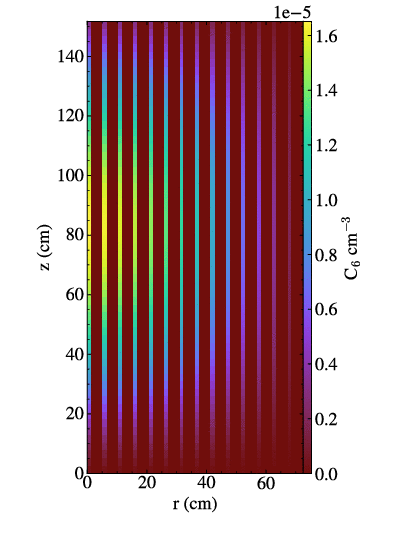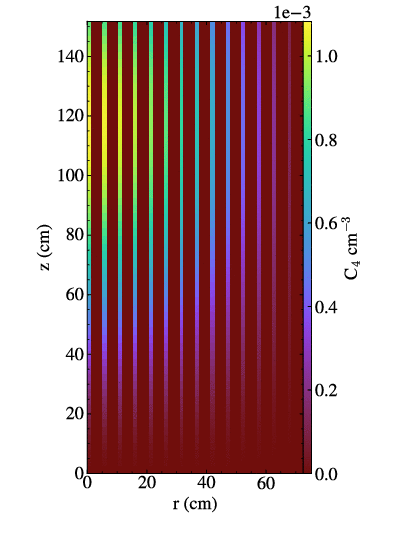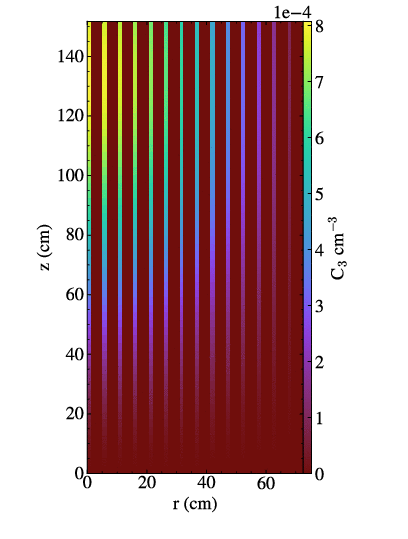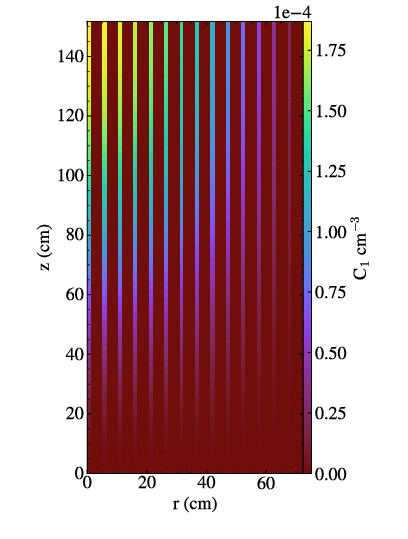
Alexander Lindsay, MSRE serpent simulation

Moltres MSRE Comparison

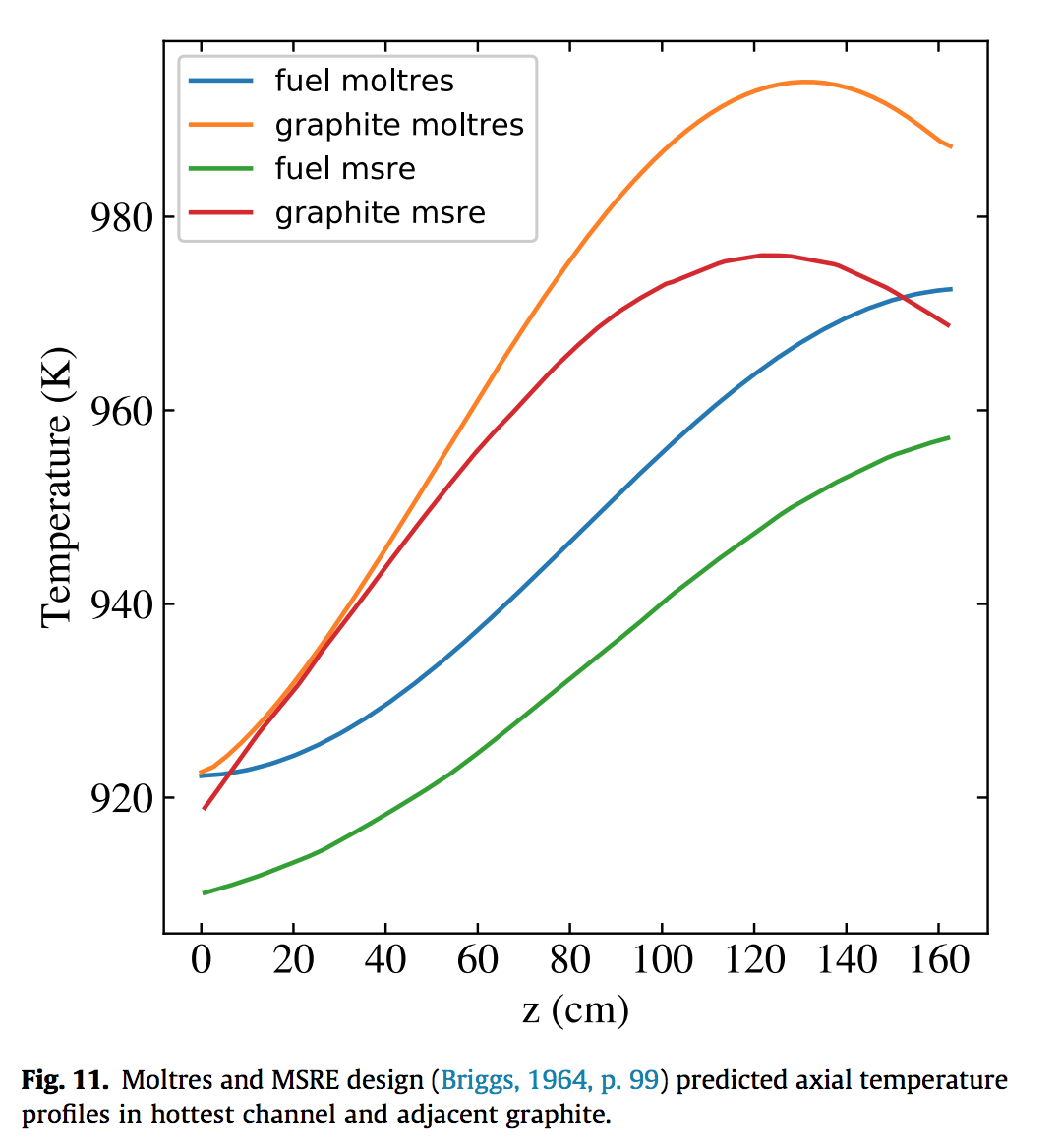
Alexander Lindsay, MSRE serpent simulation

Moltres MSRE Comparison

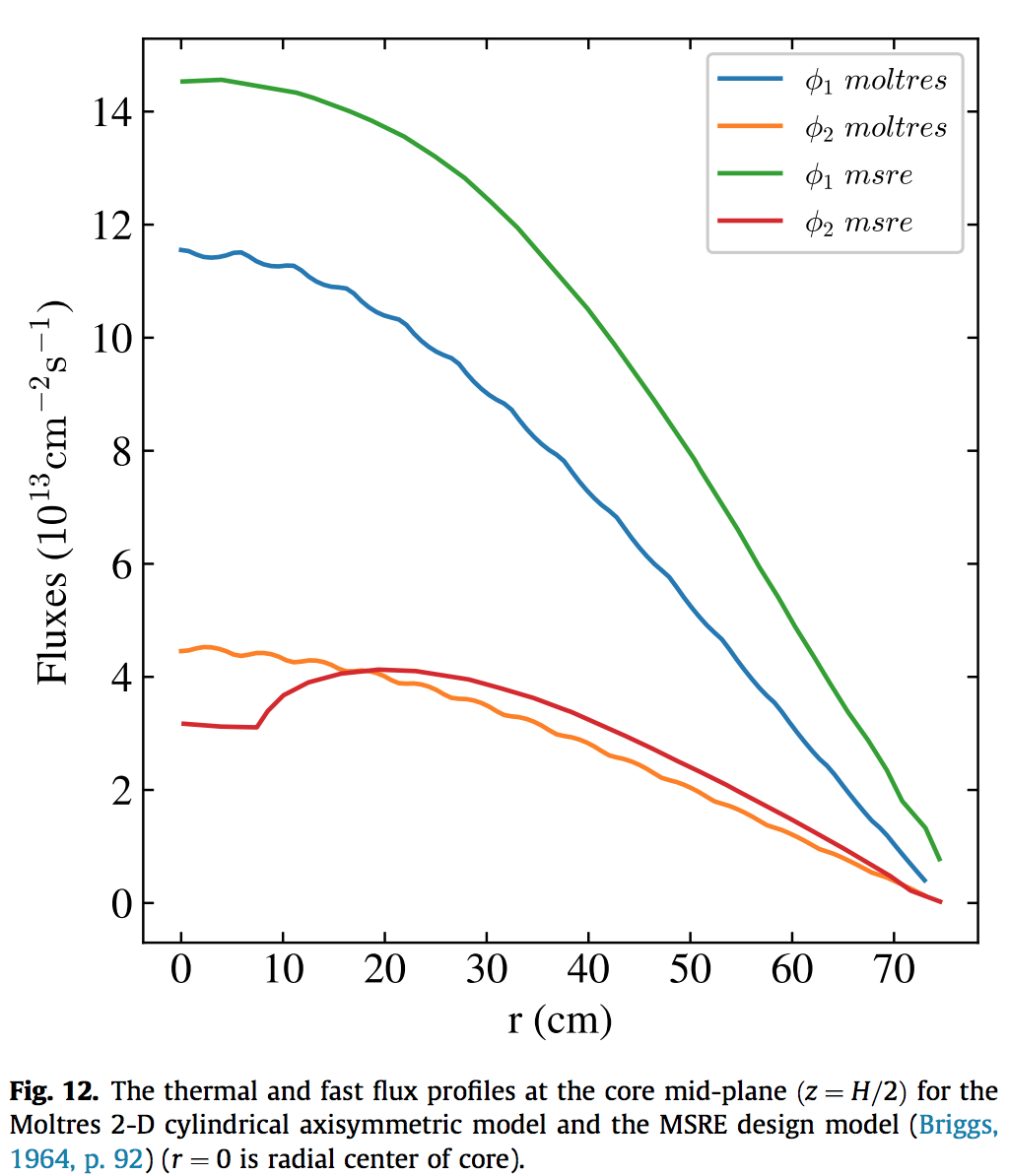
Alexander Lindsay, MSRE serpent simulation

Moltres MSRE Comparison

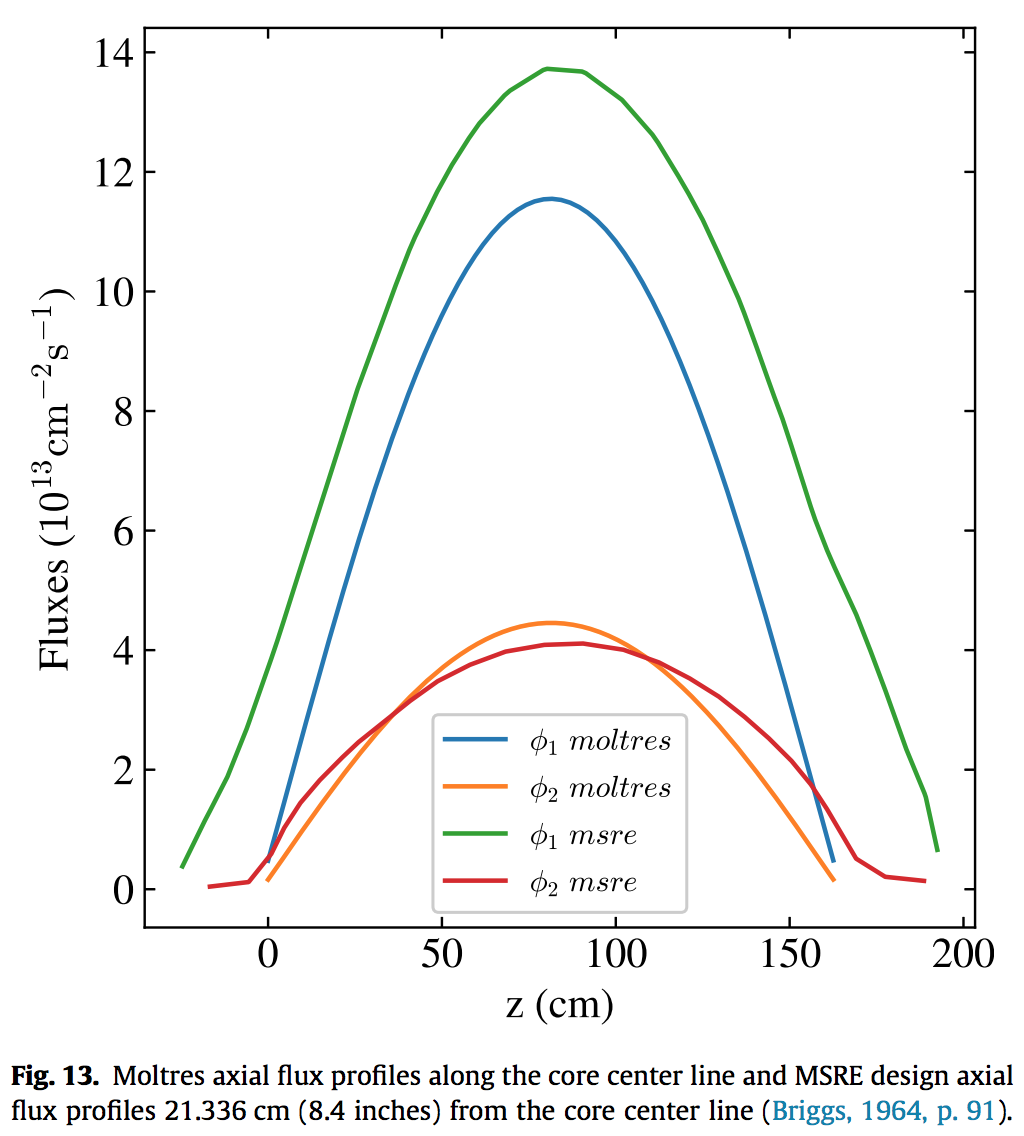
Alexander Lindsay, MSRE serpent simulation

Moltres (cross sections via Serpent)

Andrei Rykhlevskii, MSBR serpent simulation
Andrei Rykhlevskii, 2017

Moltres (cross sections via Serpent)

Alexander Lindsay, MSRE serpent simulation
Alexander Lindsay, 2016

Reactor Physics and Serpent

Andrei Rykhlevskii, MSBR fuel cycle keff
Andrei Rykhlevskii, 2017

Reactor Physics and Serpent

Andrei Rykhlevskii, MSBR fuel composition evolution
Andrei Rykhlevskii, 2017
image generated by Anthony Scopatz, Paul P.H. Wilson, and Katy Huff

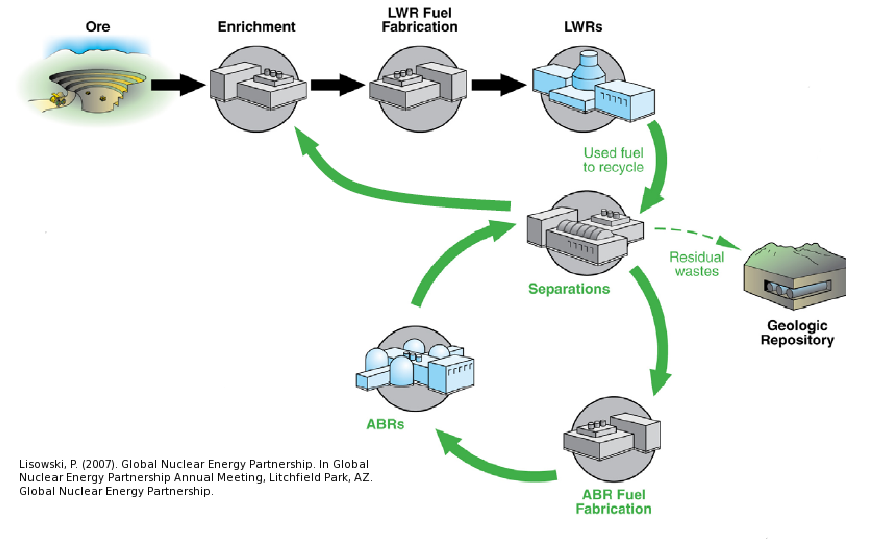
A Nuclear Fuel Cycle Simulation Framework

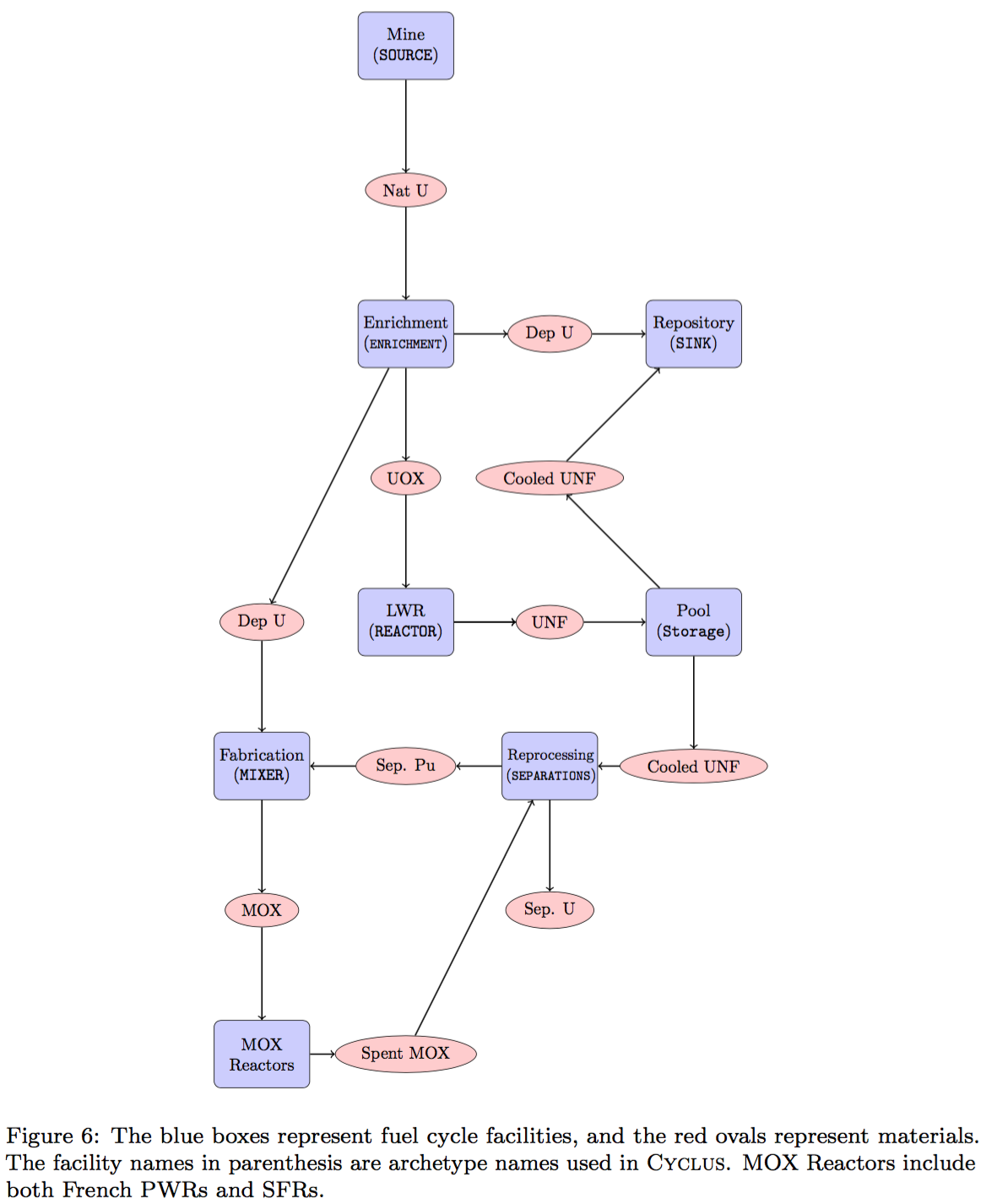
The Nuclear Fuel Cycle

Hundreds of discrete facilities mine, mill, convert, fabricate, transmute, recycle, and store nuclear material.

from Paul Lisowski

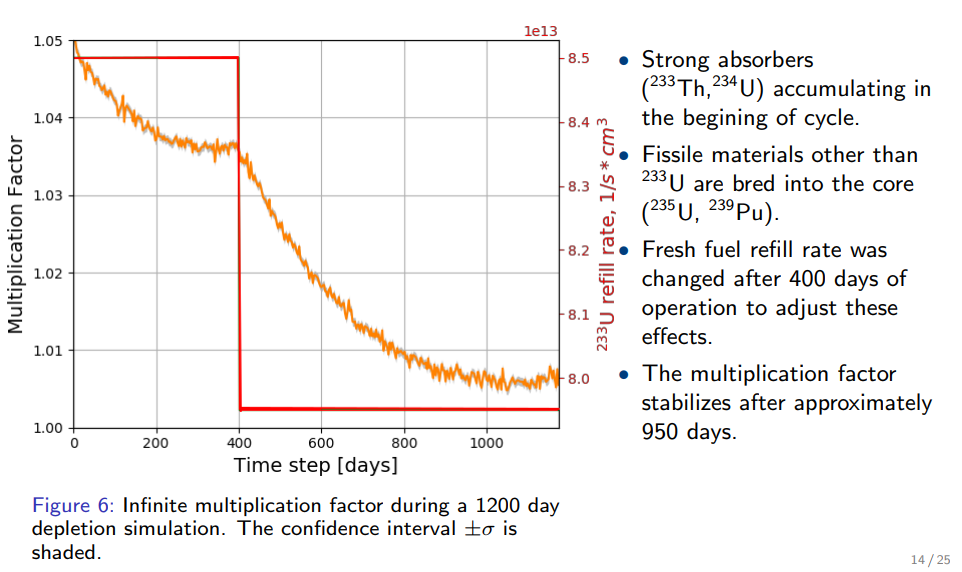
Fuel Cycle Metrics

  • Mass Flow
    • inventories, decay heat, radiotoxicity,
    • proliferation resistance and physical protection (PRPP) indices.
  • Cost
    • levelized cost of electricity,
    • facility life cycle costs.
  • Economics
    • power production, facility deployments,
    • dynamic pricing and feedback.
  • Disruptions
    • reliability, safety,
    • system robustness.

Agent Based Systems Analysis

A facility might create material.

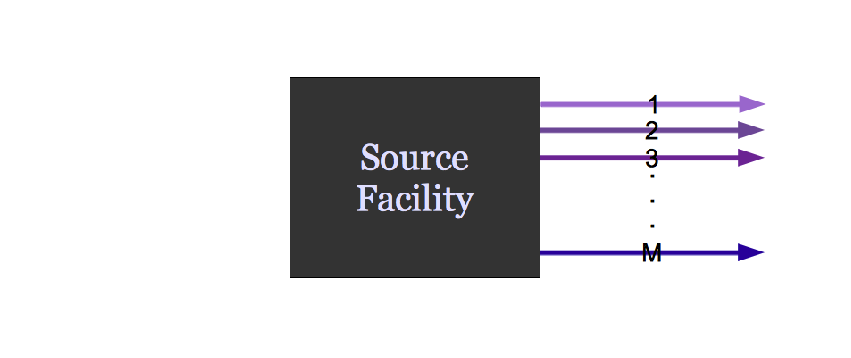
source

Agent Based Systems Analysis

It might request material.

sink

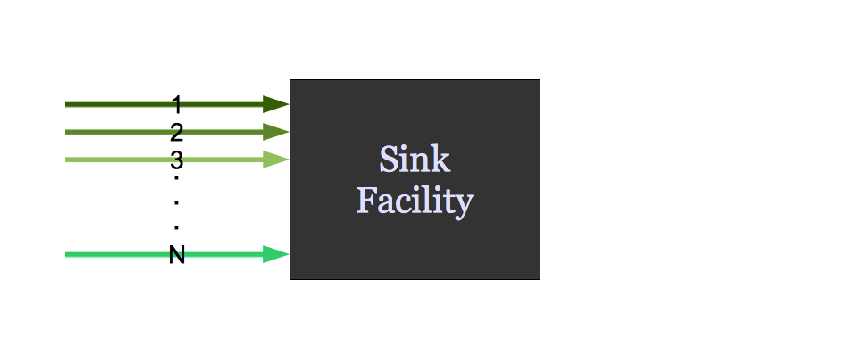
Agent Based Systems Analysis

It might do both.

fac

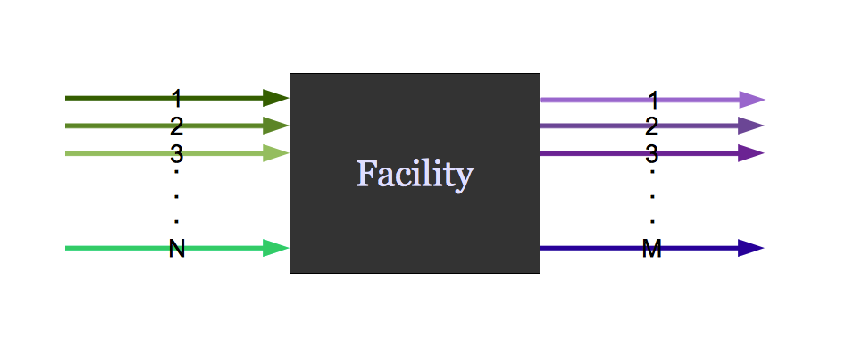
Agent Based Systems Analysis

Even simple fuel cycles have many independent agents.

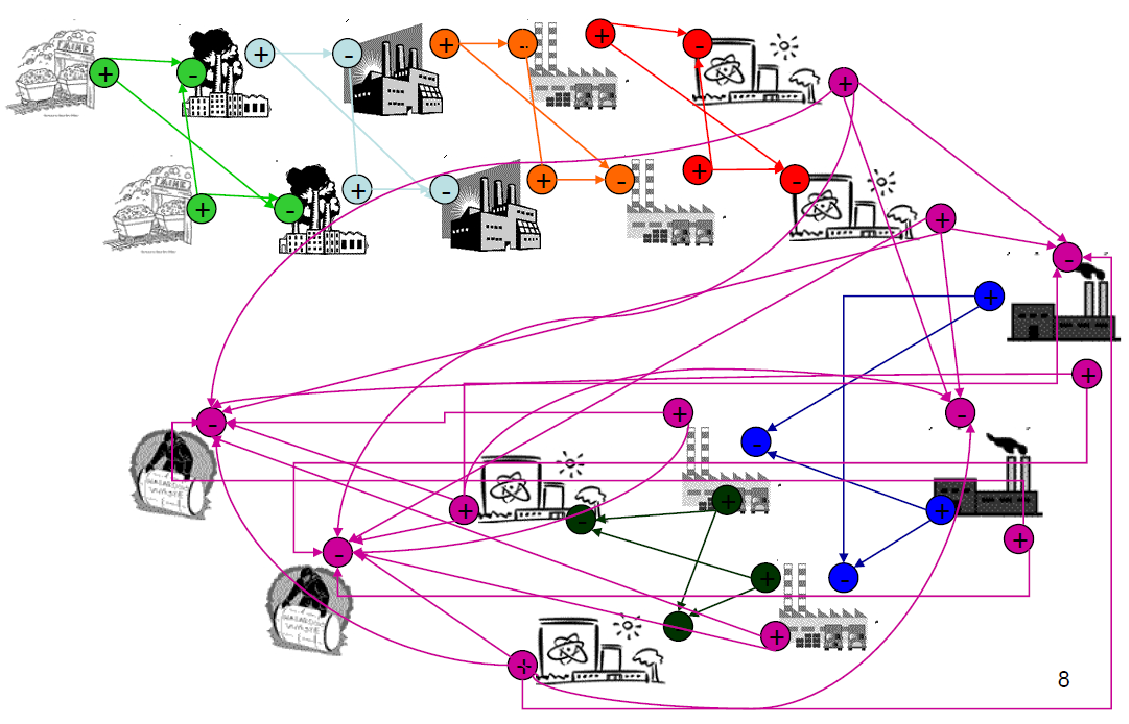
material flow

Dynamic Resource Exchange

abm \[N_i \subset N\]

Dynamic Resource Exchange

abm \[N_j \subset N\]

Dynamic Resource Exchange

abm \[N_i \cup N_j = N\]
synergistic paper

Transition Analysis

Can France transition to SFRs faster by reprocessing spent fuel from other EU nations?


  • French LWR to SFR Transition
  • Other EU Nations send all SNF to France
  • $T_0 = 1970$
  • $T_f <= 2150$
  • Annual nuclear energy demand growth: 0%
  • Sensitivity Analysis: Legacy LWR lifetimes vs. time to transition.
  • Sensitivity Analysis: SFR breeding ratio vs. time to transition.
simulation flow
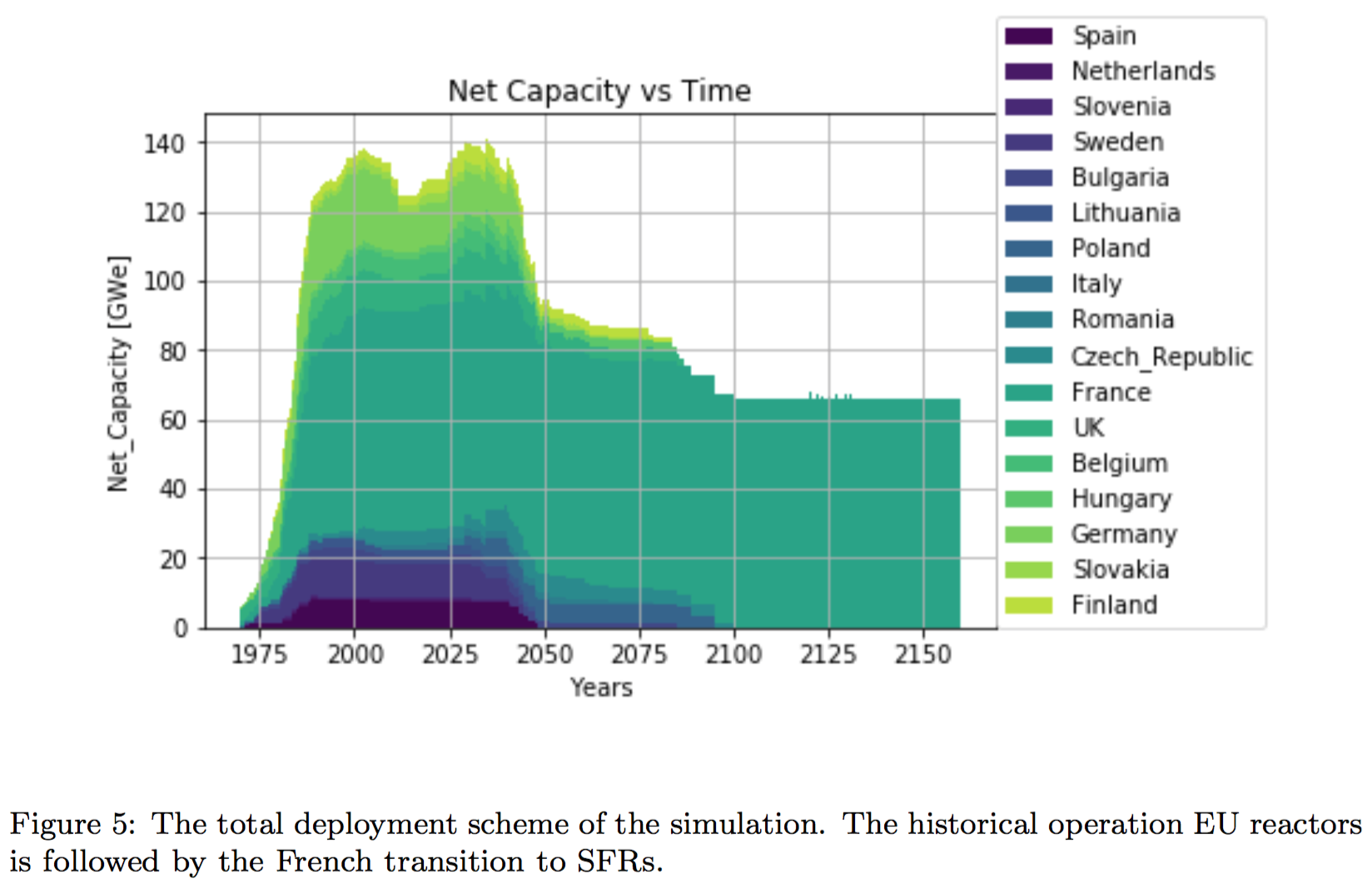
nuclear capacity in the eu, including FRs
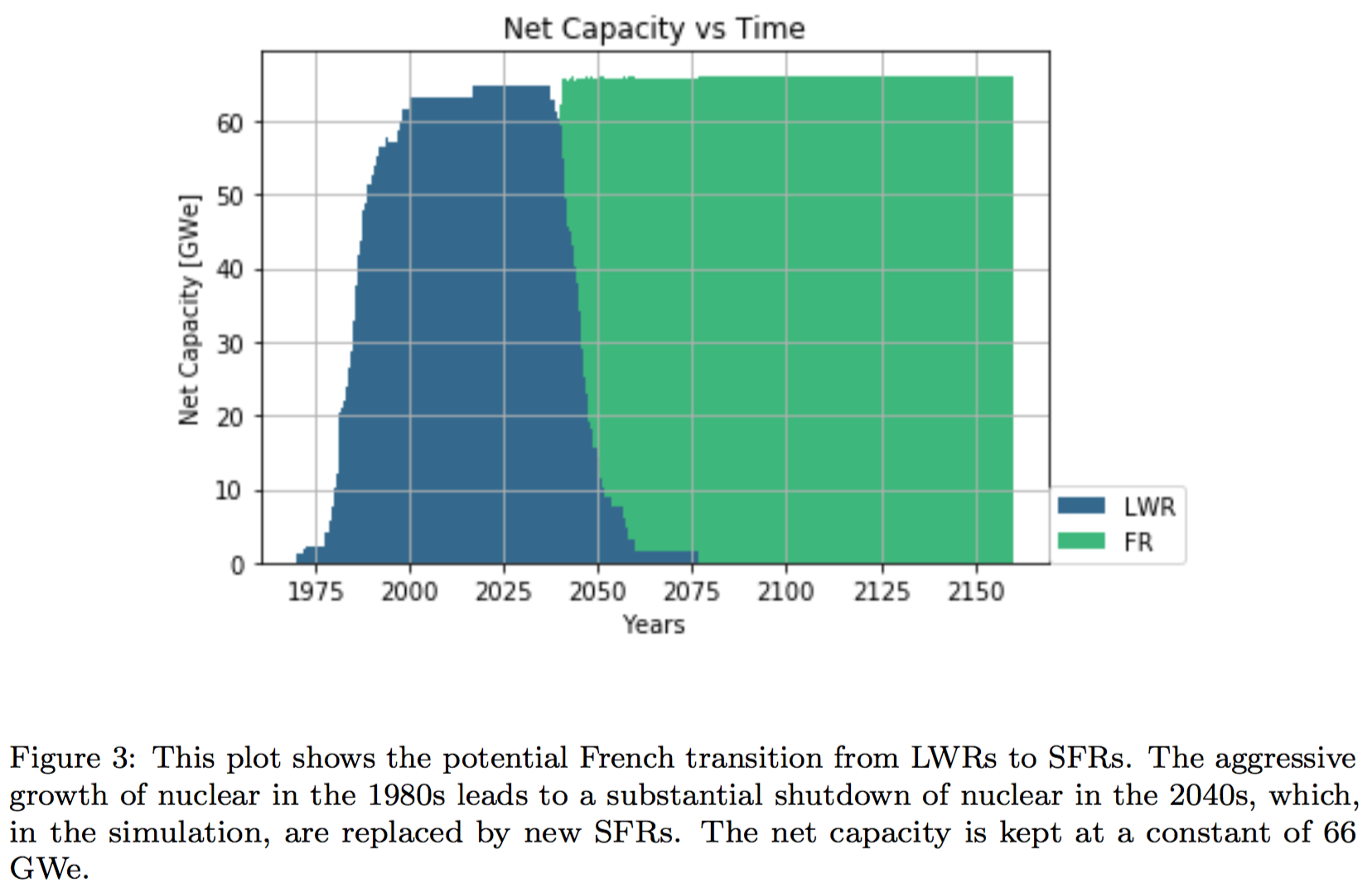
nuclear capacity in france
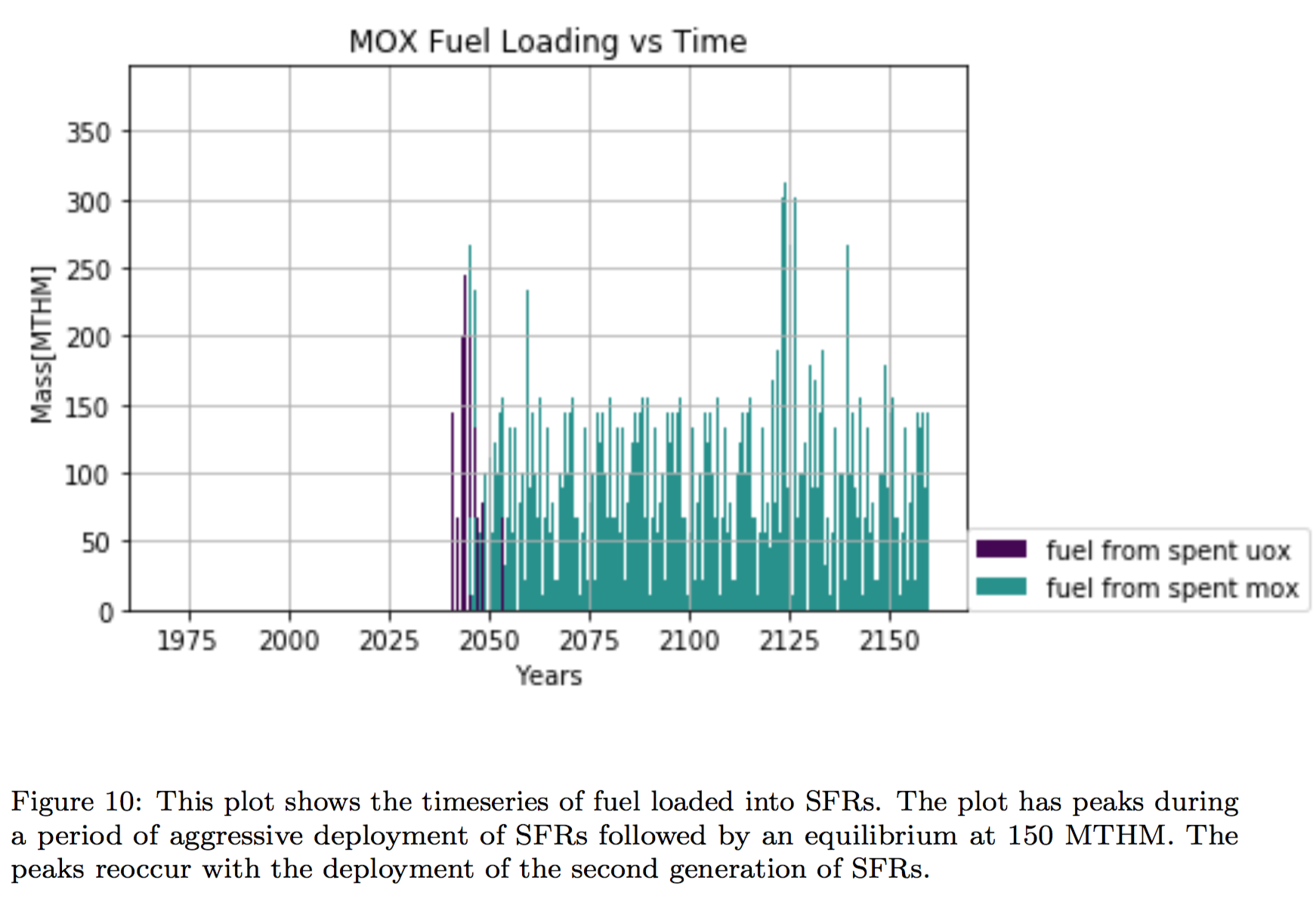
mox loading france
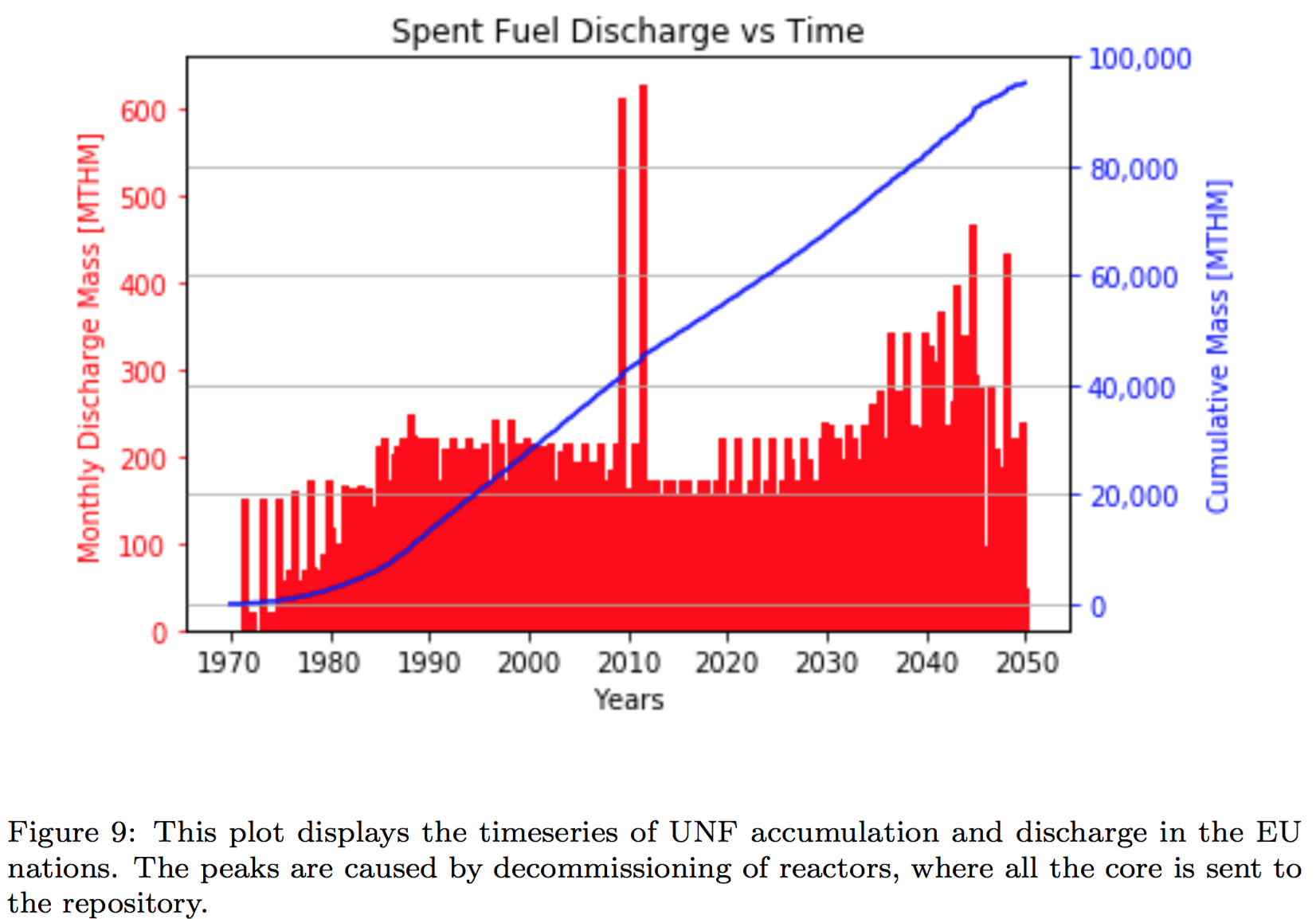
snf discharge france
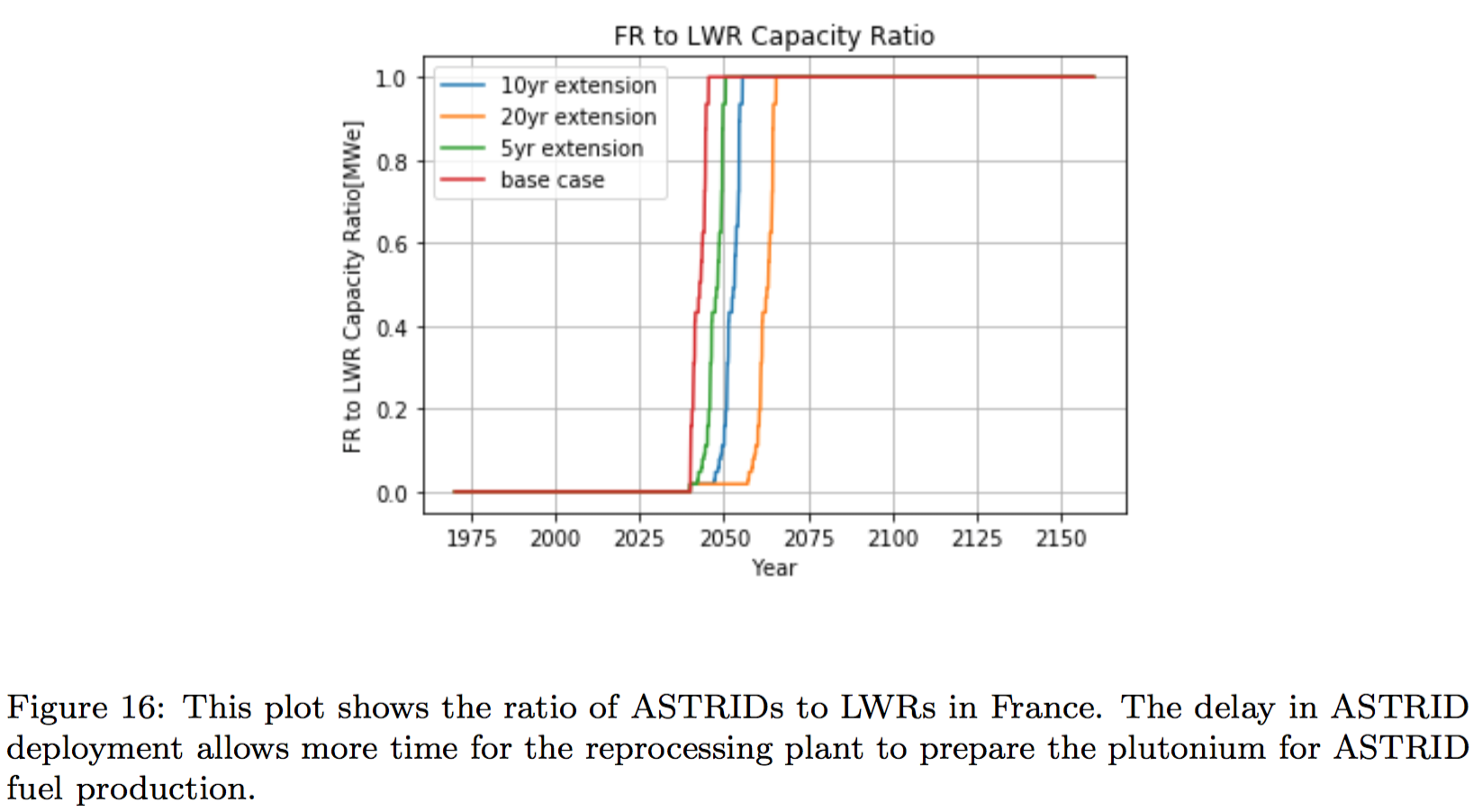
sensitivity analysis of lifetime extension impact on transition time.

Conclusions

  • The collaborative strategy speeds up the french transition.
  • In particular, the nations planning aggressive nuclear reduction will be able phase out nuclear without constructing a permanent repository.
  • Lifetime extensions slow down the transition, especially long extensions.
  • Increasing the lifetime of French LWRs decreases reprocessing demand

Links

A Few of My Favorite Things


  • C++, Python, Fortran
  • Serpent, MOOSE, ORIGEN
  • xml, markdown, rst, $\LaTeX$
  • Doxygen, sphinx
  • CMake, conda, macports
  • GoogleTest, nose
  • hdf5, sqlite
  • cython, boost, Coin
  • jekyll, reveal.js, beamer
  • yt, matplotlib, paraview

THE END

Katy Huff

katyhuff.github.io/2018-02-16-ners
Creative Commons License
Modeling and Simulation at Disparate Scales by Kathryn Huff is licensed under a Creative Commons Attribution 4.0 International License.
Based on a work at http://katyhuff.github.io/2018-02-16-ners.